题目内容
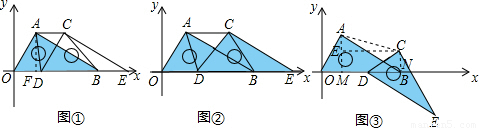
在平面直角坐标系中,两个全等的直角三角板OAB和DCE重叠在一起,∠AOB=60°,B(2,0).固定△OAB不动,将△DCE进行如下操作:(Ⅰ) 如图①,△DCE沿x轴向右平移(D点在线段AB内移动),连接AC、AD、CB,四边形ADBC的形状在不断的变化,它的面积变化吗?若不变,求出其面积;若变化,请说明理由.
(Ⅱ)如图②,当点D为OB的中点时,请你猜想四边形ADBC的形状,并说明理由.
(Ⅲ)如图③,在(Ⅱ)中,将点D固定,然后绕D点按顺时针将△DCE旋转30°,在x轴上求一点P,使|AP-CP|最大.请直接写出P点的坐标和最大值,不要求说明理由.

【答案】分析:(Ⅰ)过A点作AF⊥OB于F,作出梯形的高,求得高线长,根据平行的性质可以得到AC=OD,则利用梯形的面积公式即可求解;
(Ⅱ)利用直角三角形斜边上的中线等于斜边的一半即可证得;
(Ⅲ)当P是直线AC与x轴的交点时,|AP-CP|最大.利用待定系数法求得AC的解析式,则P的坐标可以求得.
解答:解:(Ⅰ)四边形ADBC的面积不变.
在Rt△AOB中,∵∠AOB=60°,
∴∠ABO=30°.
又B(2,0),∴OB=2,
∴OA= OB=1,
OB=1,
过A点作AF⊥OB于F,
在Rt△AOF中,∵sin60°= ,
,
∴ ,
,
由平移性质可知,AC∥OD,AC=OD
∴ ;
;
(Ⅱ)菱形,
在Rt△AOB中,∵点D为斜边OB的中点,∴OD=AD=DB.
∵AC∥DB,AC=OD=DB,
∴四边形ADBC是平行四边形,
∵AD=DB,∴四边形ADBC是菱形;
(Ⅲ)作AM⊥x轴于点M,CN⊥x轴于N.
则AM=OA•sin60°=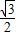 ,OM=OA•cos60°=
,OM=OA•cos60°= ,则A的坐标是:(
,则A的坐标是:( ,
, ),
),
在直角△DCN中,CN= CD=
CD= ,DN=CD•cos60°=
,DN=CD•cos60°=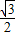 ,则ON=1+
,则ON=1+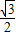 =
= ,MN=
,MN=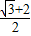 -
- =
=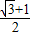 .
.
C的坐标是:(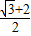 ,
, ),
),
设直线AC的解析式是y=kx+b,则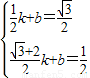 ,
,
解得: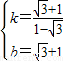 .
.
则直线的解析式是:y=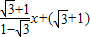 ,
,
令y=0,解得:x=2+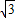 ,
,
故P的坐标是(2+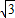 ,0).
,0).
作CE⊥AM于点E.则EC=MN=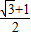 ,AE=
,AE=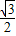 -
- =
=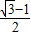 ,
,
在直角△ACE中,AC=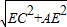 =
=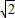 .
.
故|AP-CP|的最大值为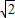 .
.
点评:本题考查了梯形的面积的计算、平行的性质以及待定系数法求函数解析式,理解P的位置是关键.
(Ⅱ)利用直角三角形斜边上的中线等于斜边的一半即可证得;
(Ⅲ)当P是直线AC与x轴的交点时,|AP-CP|最大.利用待定系数法求得AC的解析式,则P的坐标可以求得.
解答:解:(Ⅰ)四边形ADBC的面积不变.
在Rt△AOB中,∵∠AOB=60°,
∴∠ABO=30°.
又B(2,0),∴OB=2,
∴OA=
 OB=1,
OB=1,过A点作AF⊥OB于F,
在Rt△AOF中,∵sin60°=
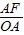 ,
,∴
 ,
,由平移性质可知,AC∥OD,AC=OD
∴
 ;
;(Ⅱ)菱形,
在Rt△AOB中,∵点D为斜边OB的中点,∴OD=AD=DB.
∵AC∥DB,AC=OD=DB,
∴四边形ADBC是平行四边形,
∵AD=DB,∴四边形ADBC是菱形;

(Ⅲ)作AM⊥x轴于点M,CN⊥x轴于N.
则AM=OA•sin60°=
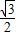 ,OM=OA•cos60°=
,OM=OA•cos60°= ,则A的坐标是:(
,则A的坐标是:( ,
, ),
),在直角△DCN中,CN=
 CD=
CD= ,DN=CD•cos60°=
,DN=CD•cos60°=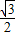 ,则ON=1+
,则ON=1+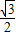 =
= ,MN=
,MN=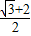 -
- =
=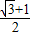 .
.C的坐标是:(
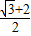 ,
, ),
),设直线AC的解析式是y=kx+b,则
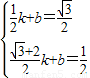 ,
,解得:
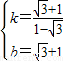 .
.则直线的解析式是:y=
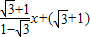 ,
,令y=0,解得:x=2+
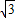 ,
,故P的坐标是(2+
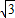 ,0).
,0).作CE⊥AM于点E.则EC=MN=
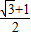 ,AE=
,AE=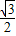 -
- =
=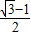 ,
,在直角△ACE中,AC=
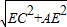 =
=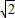 .
.故|AP-CP|的最大值为
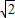 .
.点评:本题考查了梯形的面积的计算、平行的性质以及待定系数法求函数解析式,理解P的位置是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.