Question

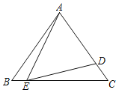
【题目】这是一道我们曾经探究过的问题：如图1．等腰直角三角形中，，．直线经过点，过作于点，过作于点．易证得≌．（无需证明），我们将这个模型称为“一线三等角”或者叫“K形图”.接下来，我们就利用这个模型来解决一些问题：

（模型应用）

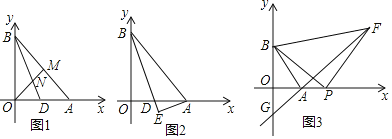
（1）如图2．已知直线l1：与与坐标轴交于点A、B．以AB为直角边作等腰直角三角形ABC，若存在，请求出C的坐标；不存在，若说明理由.

（2）如图3已知直线l1：与坐标轴交于点A、B．将直线l1绕点A逆时针旋转45°至直线l2．直线l2在x轴上方的图像上是否存在一点Q，使得△QAB是以QA为底的等腰直角三角形？若存在，请求出直线BQ的函数关系式；若不存在，说明理由.

（拓展延伸）

（3）直线AB：与轴负半轴、轴正半轴分别交于A、B两点.分别以OB、AB为边，点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE，连EF交y轴于P点，如图4,△EPB的面积是否确定？若确定，请求出具体的值；若不确定，请说明理由.

Answer 1

【答案】（1）存在，或或或；（2）存在，；（3）确定，面积是：1.

【解析】

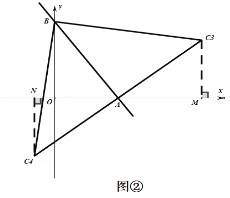
（1）存在，如图①、图②，C1、C2、C3、C4都符合，根据“一线三等角”模型，易证得三角形全等，从而求得点C的坐标；

（2）存在，过作交直线l2于，△QAB就是以QA为底边的等腰直角三角形，根据“一线三等角”模型，易证得, 从而求得点Q的坐标，继而求得直线BQ的函数关系式；

（3）确定，面积是：1.过作轴于，根据“一线三等角”模型，易证得,可求得E、F的坐标，从而求得直线EF的解析式，继而求得P点坐标，可以求得△EPB的面积.

（1）∵直线l1：与与坐标轴交于点A、B,

∴A、B的坐标分别是A(3，0)、B(0，4)，则，

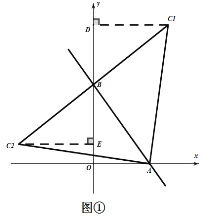
如图①：过作轴于，作轴于，

根据“一线三等角”模型，易证得

∴

∴的坐标是

如图②：过作轴于，作轴于，

根据“一线三等角”模型，易证得,

∴

∴的坐标是

（2）存在，

如图，过作交直线l2于，

由于是旋转角，

∴，

则△QAB就是以QA为底边的等腰直角三角形，

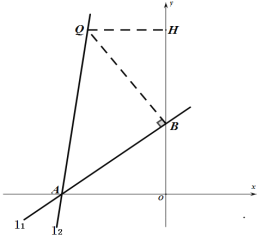
∵直线l1：与与坐标轴交于点A、B,

∴A、B的坐标分别是A(-4，0)、B(0，3)，

则，

过作轴于，

根据“一线三等角”模型，易证得

∴

∴的坐标是

设直线BQ的解析式是：

把B(0，3)，代入得,

解得：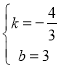

∴直线BQ的解析式是：

（3）确定，面积是：1.

∵直线AB：与轴负半轴、轴正半轴分别交于A、B两点,

∴A、B的坐标分别是A(-2，0)、B(0，1)，

则，

如图，过作轴于，

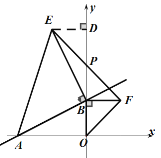
根据“一线三等角”模型，易证得

∴,

∴的坐标是

∵是等腰直角三角形，∴

∴的坐标是

设直线EF的解析式是：

把，代入得,

解得：

∴直线EF的解析式是：

∴直线EF与轴的交点坐标是