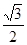题目内容
如图,将两块全等的等腰直角△ABC和△A′B′C′(其中∠C=∠C′=90°)的三角板叠放在一起,使点C′在AB的中点上,固定△ABC,将△A′B′C′绕着点C′旋转.(1)当点C在A′B′上时(如图①),求证:两块三角板重叠部分(即阴影部分)的四边形ECFC′是正方形;
(2)将图①中的△A′B′C′绕着点C′逆时针旋转某一角度后(例如图②),点C能否还在
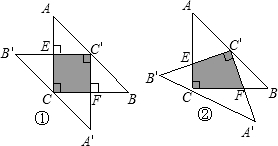 A′B′上?试说明理由.
A′B′上?试说明理由.
分析:(1)连接CC′.由△A′B′C′≌△ABC证明CC′⊥A′B′且CC′⊥
A′B′;根据C′是AB的中点来证明CC′⊥AB,且CC′=
AB;从而求得A′B′∥AB,再根据平行线的性质求得∠CC′E=∠C′CF=∠CC′F=45°,所以四边形ECFC′是菱形,又因为∠FCE=90°,所以四边形ECFC′是正方形;
(2)不能.将问题转化为CC′绕点C′顺时针旋转某一角度.
| 1 |
| 2 |
| 1 |
| 2 |
(2)不能.将问题转化为CC′绕点C′顺时针旋转某一角度.
解答: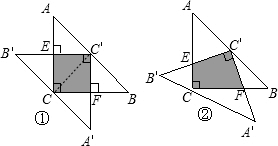 解:(1)连接CC′.
解:(1)连接CC′.
∵C′是AB的中点,
∴CC′⊥AB,且CC′=
AB;
∵△A′B′C′≌△ABC,
∴CC′⊥A′B′,且CC′=
A′B′,
∴A′B′∥AB,∠A=∠B′CE=45°(4分),
∴∠C′CE=45°,从而∠CC′E=∠C′CF=∠CC′F=45°,CE=C′E=C′F=CF=
CC′(6分),
∴四边形ECFC′是菱形,
又∠FCE=90°,
∴四边形ECFC′是正方形(7分);
(2)不能(8分),问题中“△A′B′C′绕着点C′逆时针旋转某一角度”相当于“CC′绕点C′顺时针旋转某一角度”,由于三角形的高最短且唯一,垂线段(三角形的高)最短,所以C将不再在A′B′上(9分).
 解:(1)连接CC′.
解:(1)连接CC′.∵C′是AB的中点,
∴CC′⊥AB,且CC′=
| 1 |
| 2 |
∵△A′B′C′≌△ABC,
∴CC′⊥A′B′,且CC′=
| 1 |
| 2 |
∴A′B′∥AB,∠A=∠B′CE=45°(4分),
∴∠C′CE=45°,从而∠CC′E=∠C′CF=∠CC′F=45°,CE=C′E=C′F=CF=
| ||
| 2 |
∴四边形ECFC′是菱形,
又∠FCE=90°,
∴四边形ECFC′是正方形(7分);
(2)不能(8分),问题中“△A′B′C′绕着点C′逆时针旋转某一角度”相当于“CC′绕点C′顺时针旋转某一角度”,由于三角形的高最短且唯一,垂线段(三角形的高)最短,所以C将不再在A′B′上(9分).
点评:本题主要考查了旋转的性质、全等三角形的判定与性质及正方形的性质.解答此题时,采用了“转化的思想”数学思想,即将(2)中的问题转化为CC′绕点C′顺时针旋转某一角度,然后利用“两点间垂线段最短的”几何知识来解答问题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
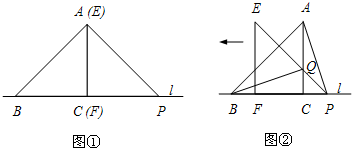
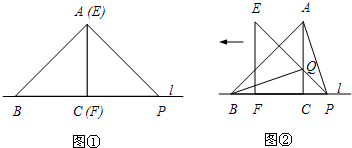
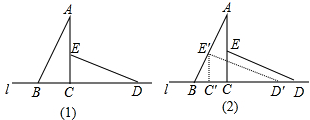
 .将△ECD沿直线l向左平移到图(2)的位置,使E点落在AB上,则CC′=( )
.将△ECD沿直线l向左平移到图(2)的位置,使E点落在AB上,则CC′=( )