题目内容
已知Rt△ABC∽Rt△A′B′C′，∠C=∠C′=90°，且AB=2A′B′，则sinA与sinA′的关系为
- A.sinA=2sinA′
- B.2sinA=sinA′
- C.sinA=sinA′
- D.不确定
C
分析：由于Rt△ABC∽Rt△A′B′C′，则∠A=∠A′．根据三角函数值只与角的大小有关即可求解．
解答：由于Rt△ABC∽Rt△A′B′C′，则∠A=∠A′，
∴sinA=sinA′．
故选C．
点评：三角函数值只与角的大小有关．
分析：由于Rt△ABC∽Rt△A′B′C′，则∠A=∠A′．根据三角函数值只与角的大小有关即可求解．
解答：由于Rt△ABC∽Rt△A′B′C′，则∠A=∠A′，
∴sinA=sinA′．
故选C．
点评：三角函数值只与角的大小有关．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知Rt△ABC中，∠C=90°，AC=8cm，BC=6cm．则其内心和外心之间的距离是（ ）
| A、10cm | ||
| B、5cm | ||
C、
| ||
| D、2cm |
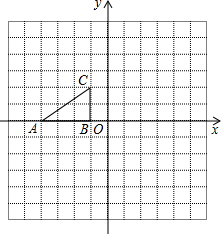如图，每个小方格都是边长为1个单位的正方形．Rt△ABC 的顶点在格 点上，建立平面直角坐标系后，点A的坐标为（-4，0），点B的坐标为（-1，0）．已知Rt△ABC和Rt△A1B1C1关于y轴对称，Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称．