题目内容
 如图,已知抛物线 y=-x2+bx+c过点A(2,0),对称轴为y轴,顶点为P.
如图,已知抛物线 y=-x2+bx+c过点A(2,0),对称轴为y轴,顶点为P.(1)求该抛物线的表达式,写出其顶点P的坐标,并画出其大致图象;
(2)把该抛物线先向右平移m个单位,再向下平移m个单位(m>0 ),记新抛物线的顶点为B,与y轴的交点为C.
①试用m的代数式表示点B、点C的坐标; ②若∠OBC=45°,试求m的值.
分析:(1)小题的解题思路是把点A的坐标和对称轴(X=0)代入抛物线y=-x2+bx+c就可求出表达式和顶点坐标;
(2)小题是根据平移规律(上加下减右减左加),即可求出新抛物线的顶点B的坐标及与y轴的交点C坐标;
②小题是先证明两三角形相似,再利用相似三角形的边之比相等,即可求出m的值.
(2)小题是根据平移规律(上加下减右减左加),即可求出新抛物线的顶点B的坐标及与y轴的交点C坐标;
②小题是先证明两三角形相似,再利用相似三角形的边之比相等,即可求出m的值.
解答:解:(1)∵抛物线y=-x2+bx+c过点A(2,0),对称轴为y轴,代入得: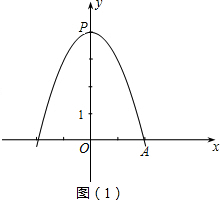
∴b=0,c=4,
∴y=-x2+4,
当x=0时y=4,
P的坐标是(0,4),
大致图象如图(1):
所以:该抛物线的表达式是:y=-x2+4,其顶点P的坐标是:(0,4).
(2)①∵抛物线先向右平移m个单位,再向下平移m个单位(m>0)
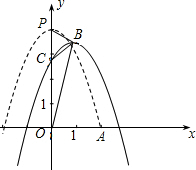 ∴B(m,4-m),
∴B(m,4-m),
∵y=-(x-m)2+4-m,
当x=0时代入得:y=-m2-m+4,
∴C(0,-m2-m+4),
所以,用m的代数式表示点B的坐标是:(m,4-m),点C的坐标是:(0,-m2-m+4).
②过B作BN⊥y轴于N,
∵由已知,抛物线先向右平移m个单位,再向下平移m个单位,
∴PN=BN=m,∠BNP=90°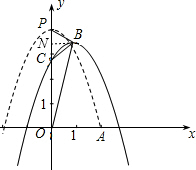
∠OPB=∠PBN=45°,又∠OBC=45°,
∴∠OPB=∠CBO=45°
又∵∠POB=∠POB,
∴△OCB与△OBP相似.
当点C在y轴正半轴,即-m2-m+4>0时BO2=OC•OP,
∵BO2=2m2-8m+16,OC=-m2-m+4,OP=4.
解得m1=0(舍去),m2=
,
另解:过点C作CD⊥OB于点D,过点B作BE⊥OC于点E,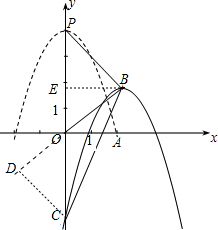
同理利用△CPB∽△CBO
当点C在y轴负半轴,点-m2-m+4<0时BC2=OC•CP,
∵BC2=m2+m4,OC=m2+m-4,CP=m2+m.
解得m1=0(舍去),m2,3=1±
(负根舍去)
∴m=1+
,
所以m的值是
或1+
.

|
∴b=0,c=4,
∴y=-x2+4,
当x=0时y=4,
P的坐标是(0,4),
大致图象如图(1):
所以:该抛物线的表达式是:y=-x2+4,其顶点P的坐标是:(0,4).
(2)①∵抛物线先向右平移m个单位,再向下平移m个单位(m>0)
 ∴B(m,4-m),
∴B(m,4-m),∵y=-(x-m)2+4-m,
当x=0时代入得:y=-m2-m+4,
∴C(0,-m2-m+4),
所以,用m的代数式表示点B的坐标是:(m,4-m),点C的坐标是:(0,-m2-m+4).
②过B作BN⊥y轴于N,
∵由已知,抛物线先向右平移m个单位,再向下平移m个单位,
∴PN=BN=m,∠BNP=90°

∠OPB=∠PBN=45°,又∠OBC=45°,
∴∠OPB=∠CBO=45°
又∵∠POB=∠POB,
∴△OCB与△OBP相似.
当点C在y轴正半轴,即-m2-m+4>0时BO2=OC•OP,
∵BO2=2m2-8m+16,OC=-m2-m+4,OP=4.
解得m1=0(舍去),m2=
| 2 |
| 3 |
另解:过点C作CD⊥OB于点D,过点B作BE⊥OC于点E,

同理利用△CPB∽△CBO
当点C在y轴负半轴,点-m2-m+4<0时BC2=OC•CP,
∵BC2=m2+m4,OC=m2+m-4,CP=m2+m.
解得m1=0(舍去),m2,3=1±
| 3 |
∴m=1+
| 3 |
所以m的值是
| 2 |
| 3 |
| 3 |
点评:解此题主要考查对求抛物线的顶点坐标和与y轴交点坐标的掌握,能应用平移规律求解析式,关键是把二次函数的图象转化成相似三角形利用相似三角形的性质来解决.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 C(0,3).
C(0,3). 、C(0,-3)两点,与x轴交于另一点B.
、C(0,-3)两点,与x轴交于另一点B. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B. 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;