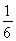题目内容
已知∠α,∠β都是钝角,甲、乙、丙、丁四人计算
(∠α+∠β)的结果依次是50°,26°,72°,90°,试判断谁的计算是正确的.
| 1 | 6 |
分析:根据∠α,∠β都是钝角,判断出∠α+∠β的取值范围,再将50°,26°,72°,90°分别代入验证即可.
解答:解:∵∠α,∠β都是钝角,
∴180°<∠α+∠β<360°.
当结果是50°时,∠α+∠β=6×50°=300°;
当结果是26°时,∠α+∠β=6×26°=156°;
当结果是72°时,∠α+∠β=6×72°=432°;
当结果是90°时,∠α+∠β=6×90°=540°;
所以计算结果是50°时,计算是正确的,即甲的计算结果是正确的.
∴180°<∠α+∠β<360°.
当结果是50°时,∠α+∠β=6×50°=300°;
当结果是26°时,∠α+∠β=6×26°=156°;
当结果是72°时,∠α+∠β=6×72°=432°;
当结果是90°时,∠α+∠β=6×90°=540°;
所以计算结果是50°时,计算是正确的,即甲的计算结果是正确的.
点评:本题考查了角的计算,判断出∠α+∠β的取值范围是关键一步.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目