题目内容
已知α、β都是钝角,甲、乙、丙、丁四人计算
(α+β)的结果依次为26°、50°、72°、90°,其中有正确的结果,那么计算正确的人是
| 1 | 6 |
乙
乙
.分析:求出α+β的范围,求出
(α+β)的范围,即可得出答案.
| 1 |
| 6 |
解答:解:∵α、β都是钝角,
∴90°<α<180°,90°<β<180°,
∴180°<α+β<360°,
∴都乘以
得:30°<α+β<60°,
∵甲、乙、丙、丁四人计算
(α+β)的结果依次为26°、50°、72°、90°,
∴只有乙计算正确,
故答案为:乙.
∴90°<α<180°,90°<β<180°,
∴180°<α+β<360°,
∴都乘以
| 1 |
| 6 |
∵甲、乙、丙、丁四人计算
| 1 |
| 6 |
∴只有乙计算正确,
故答案为:乙.
点评:本题考查了角的有关计算的应用,关键是求
(α+β)的范围.
| 1 |
| 6 |

练习册系列答案
相关题目
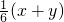 的结果依次为50°,26°,72°,90°,你认为结果正确的是
的结果依次为50°,26°,72°,90°,你认为结果正确的是