题目内容
正多边形的边长为2，中心到边的距离为
，则这个正多边形的边数为______．
| 3 |
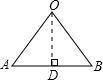
如图，设正多边形的中心为O点，AB为边长，
过O点作OD⊥AB，垂足为D，
依题意得AB=2，OD=
，
∵OA=OB，
∴AD=
AB=1，∠AOB=2∠AOD，
在Rt△AOD中，tan∠AOD=
=
=
，
∴∠AOD=30°，
∴∠AOB=2∠AOD=60°，
∴正多边形的边数=
=6．
故答案为：6．
过O点作OD⊥AB，垂足为D，
依题意得AB=2，OD=
| 3 |
∵OA=OB，
∴AD=
| 1 |
| 2 |
在Rt△AOD中，tan∠AOD=
| AD |
| OD |
| 1 | ||
|
| ||
| 3 |
∴∠AOD=30°，
∴∠AOB=2∠AOD=60°，
∴正多边形的边数=
| 360° |
| 60° |
故答案为：6．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
