题目内容
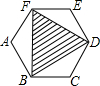
圆的两条弦AB、AC分别是它的内接正三角形与内接正五边形的边长，则∠BAC等于（ ）
| A．24°或84° | B．54° | C．32°或72° | D．36° |
如图，连结OA、OB、OC．
∵∠AOC=
=72°，OA=OC，
∴∠OAC=
=54°．
∵∠AOB=
=120°，OA=OB，
∴∠OAB=
=30°．
分两种情况：
①当AB、AC都在OA同侧时，如图1，
∠BAC=∠OAC-∠OAB=54°-30°=24°；
②当AB、AC在OA两侧时，如图2，
∠BAC=∠OAC+∠OAB=54°+30°=84°．
故选A．
∵∠AOC=
| 360° |
| 5 |
∴∠OAC=
| 180°-72° |
| 2 |
∵∠AOB=
| 360° |
| 3 |
∴∠OAB=
| 180°-120° |
| 2 |
分两种情况：①当AB、AC都在OA同侧时，如图1，
∠BAC=∠OAC-∠OAB=54°-30°=24°；
②当AB、AC在OA两侧时，如图2，
∠BAC=∠OAC+∠OAB=54°+30°=84°．
故选A．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
BD的延长线，连接CD．
