题目内容

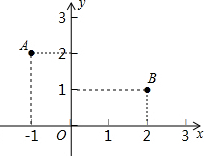精英家教网如图，点A的坐标为（-1，2），点B的坐标为（2，1），有一点C在x轴上移动，则点C到A、B两点的距离之和的最小值为（　　）
A、3
2
B、4
C、3
D、4
2
分析：作点A关于x轴的对称点A′，连接A′B交x轴于点C，则线段A′B的长即为点C到A、B两点的距离之和的最小值．
解答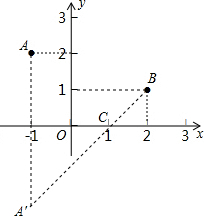：精英家教网解：作点A关于x轴的对称点A′，连接A′B交x轴于点C，
∵A（-1，2），
∴A′（-1，-2），
∵B（2，1），
∴A′B=
(2+1)2+(1+2)2
=3
2
．
故选A．
点评：本题考查的是轴对称-最短路线问题，熟知两点之间，线段最短是解答此题的关键．
练习册系列答案
相关题目
（2012•桂平市三模）如图，点P的坐标为（2，
3
2
），过点P作x轴的平行线交y轴于点A，交反比例函数y=
k
x
（x＞0）的图象于点N；作PM⊥AN交反比例函数y=
k
x
（x＞0）的图象于点M，PN=4．
（1）求反比例函数和直线AM的解析式；
（2）求△APM的面积．
已知：在直角坐标系中，点C的坐标为（0，-2），点A与点B在x轴上，且点A与点B的横坐标是方程x2-3x-4=0的两个根，点A在点B的左侧．
（1）求经过A、B、C三点的抛物线的关系式．
（2）如图，点D的坐标为（2，0），点P（m，n）是该抛物线上的一个动点（其中m＞0，n＜0），连接DP交BC于点E．
①当△BDE是等腰三角形时，直接写出此时点E的坐标．
②连接CD、CP，△CDP是否有最大面积？若有，求出△CDP的最大面积和此时点P的坐标；若没有，请说明理由．
如图，点A的坐标为（-1，0），点B在直线y=x上运动，当线段AB最短时，点B的坐标为
（-
1
2
，-
1
2
）
（-
1
2
，-
1
2
）
．
如图，点A的坐标为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网