题目内容
 如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为
如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为(-
,-
)
| 1 |
| 2 |
| 1 |
| 2 |
(-
,-
)
.| 1 |
| 2 |
| 1 |
| 2 |
分析:先过点A作AB′⊥OB,垂足为点B′,由于点B在直线y=x上运动,所以△AOB′是等腰直角三角形,由勾股定理求出OB′的长即可得出点B′的坐标.
解答: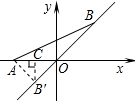 解:先过点A作AB′⊥OB,垂足为点B′,由垂线段最短可知,当B′与点B重合时AB最短,
解:先过点A作AB′⊥OB,垂足为点B′,由垂线段最短可知,当B′与点B重合时AB最短,
∵点B在直线y=x上运动,
∴△AOB′是等腰直角三角形,
过B′作B′C⊥x轴,垂足为C,
∴△B′CO为等腰直角三角形,
∵点A的坐标为(-1,0),
∴OC=CB′=
OA=
×1=
,
∴B′坐标为(-
,-
),
即当线段AB最短时,点B的坐标为(-
,-
).
故答案为:(-
,-
).
 解:先过点A作AB′⊥OB,垂足为点B′,由垂线段最短可知,当B′与点B重合时AB最短,
解:先过点A作AB′⊥OB,垂足为点B′,由垂线段最短可知,当B′与点B重合时AB最短,∵点B在直线y=x上运动,
∴△AOB′是等腰直角三角形,
过B′作B′C⊥x轴,垂足为C,
∴△B′CO为等腰直角三角形,
∵点A的坐标为(-1,0),
∴OC=CB′=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴B′坐标为(-
| 1 |
| 2 |
| 1 |
| 2 |
即当线段AB最短时,点B的坐标为(-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了一次函数的性质、垂线段最短和等腰直角三角形的性质,找到表示B′点坐标的等腰直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•桂平市三模)如图,点P的坐标为(2,
(2012•桂平市三模)如图,点P的坐标为(2, 已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧.
已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧. 如图,点A的坐标为( )
如图,点A的坐标为( )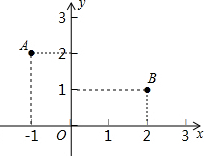 如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )
如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )