题目内容
【题目】如图,已知∠BAD=∠DAC=9°,AD⊥AE,且AB+AC=BE,则∠B的大小是( )
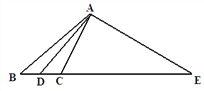
A.42°B.44°C.46 °D.48°
【答案】D
【解析】
如图,延长BA到F,使AF=AC,连接EF,
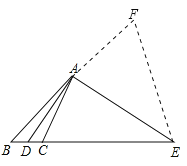
∵AB+AC=BE,
∴AB+AF=BE,即BF=BE,
∴∠F=∠BEF=![]() ,
,
∵AD⊥AE,∴∠DAE=90°,
∵∠BAD=∠DAC=9°,
∴∠FAE=180°-(∠BAD+∠DAE)=180°-(9°+90°)=81°,
∠CAE=∠DAE-∠DAC=90°-9°=81°,
∴∠FAE=∠CAE,
在△AFE和△ACE中, ,
,
∴△AFE≌△ACE(SAS),
∴∠F=∠ACE,
又∵∠ACE为△ABC的外角,
∴∠ACE=∠B+∠BAC=∠B+18°,
∴∠F=∠B+18°,
∴∠B+18°=![]() ,
,
解得∠B=48°.
故选D.

练习册系列答案
相关题目





