Question

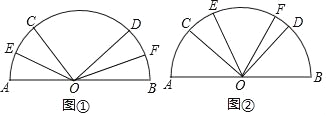
【题目】点C，D是半圆弧上的两个动点，在运动的过程中保持∠COD＝100°.

(1)如图①，OE平分∠AOC，OF平分∠BOD，求∠EOF的度数；

(2)如图②，已知∠AOC的度数为x，OE平分∠AOD，OF平分∠BOC，求∠EOF的度数．

Answer 1

【答案】(1)∠EOF＝140°；(2)∠EOF＝40°.

【解析】

(1)由角平分线的定义可得∠EOC＝∠AOE＝∠AOC，∠DOF＝∠BOF＝∠BOD，则可求∠EOF的度数；

(2)由题意可得∠AOD＝(100+x)°，∠BOC＝(180﹣x)°，由角平分线的性质可得∠DOE＝∠AOD，∠COF＝∠BOC，即可求∠EOF的度数．

解：(1)∵OE平分∠AOC，OF平分∠BOD，

∴∠EOC＝∠AOE＝∠AOC，∠DOF＝∠BOF＝∠BOD，

∵∠COD＝100°

∴∠AOC+∠DOB＝180°﹣∠COD＝80°，

∵∠EOF＝∠COE+∠DOF+∠COD

∴∠EOF＝(∠AOC+∠BOD)+∠COD＝140°

(2)∵∠AOC＝x°

∴∠AOD＝(100+x)°，∠BOC＝(180﹣x)°

∵OE平分∠AOD，OF平分∠BOC，

∴∠DOE＝∠AOD，∠COF＝∠BOC.

∵∠EOF＝∠DOE+∠COF﹣∠COD

∴∠EOF＝(100+x+180﹣x)﹣100＝40°