题目内容
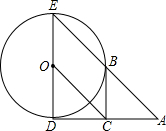 (2013•德州)如图,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCOE是平行四边形.
(2013•德州)如图,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCOE是平行四边形.(1)求AD的长;
(2)BC是⊙O的切线吗?若是,给出证明;若不是,说明理由.
分析:(1)连接BD,由ED为圆O的直径,利用直径所对的圆周角为直角得到∠DBE为直角,由BCOE为平行四边形,得到BC与OE平行,且BC=OE=1,在直角三角形ABD中,C为AD的中点,利用斜边上的中线等于斜边的一半求出AD的长即可;
(2)连接OB,由BC与OD平行,BC=OD,得到四边形BCDO为平行四边形,由AD为圆的切线,利用切线的性质得到OD垂直于AD,可得出四边形BCDO为矩形,利用矩形的性质得到OB垂直于BC,即可得出BC为圆O的切线.
(2)连接OB,由BC与OD平行,BC=OD,得到四边形BCDO为平行四边形,由AD为圆的切线,利用切线的性质得到OD垂直于AD,可得出四边形BCDO为矩形,利用矩形的性质得到OB垂直于BC,即可得出BC为圆O的切线.
解答: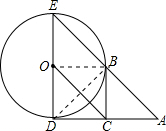 解:(1)连接BD,∵DE是直径∴∠DBE=90°,
解:(1)连接BD,∵DE是直径∴∠DBE=90°,
∵四边形BCOE为平行四边形,
∴BC∥OE,BC=OE=1,
在Rt△ABD中,C为AD的中点,
∴BC=
AD=1,
则AD=2;
(2)是,理由如下:
如图,连接OB.∵BC∥OD,BC=OD,
∴四边形BCDO为平行四边形,
∵AD为圆O的切线,
∴OD⊥AD,
∴四边形BCDO为矩形,
∴OB⊥BC,
则BC为圆O的切线.
 解:(1)连接BD,∵DE是直径∴∠DBE=90°,
解:(1)连接BD,∵DE是直径∴∠DBE=90°,∵四边形BCOE为平行四边形,
∴BC∥OE,BC=OE=1,
在Rt△ABD中,C为AD的中点,
∴BC=
| 1 |
| 2 |
则AD=2;
(2)是,理由如下:
如图,连接OB.∵BC∥OD,BC=OD,
∴四边形BCDO为平行四边形,
∵AD为圆O的切线,
∴OD⊥AD,
∴四边形BCDO为矩形,
∴OB⊥BC,
则BC为圆O的切线.
点评:此题考查了切线的判定与性质,直角三角形斜边上的中线性质,以及平行四边形的判定与性质,熟练掌握切线的判定与性质是解本题的关键.

练习册系列答案
相关题目
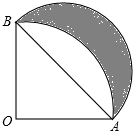 (2013•德州)如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中阴影部分的面积为( )
(2013•德州)如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中阴影部分的面积为( ) (2013•德州)如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出这一现象的原因
(2013•德州)如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出这一现象的原因 (2013•德州)如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:
(2013•德州)如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论: