题目内容
如图，直线l与坐标轴分别交于A、B两点，∠BAO=45°，点A坐标为(8,0)．动点P从点O出发，沿折线段OBA运动，到点A停止；同时动点Q也从点O出发，沿线段OA运动，到点A停止；它们的运动速度均为每秒1个单位长度．
(1)求直线AB的函数关系式；
(2)若点A、B、O与平面内点E组成的图形是平行四边形，请直接写出点E的坐标；
(3)在运动过程中，当P、Q的距离为2时，求点P的坐标．
（1）y=-x+8；（2）（2）(8，8)、 (－8，8)、(8，－8)；（3）(0，
)、 (8－，2)．
解析试题分析：（1）根据OA和OB的长度可求出A、B两点的坐标；将A、B两点的坐标代入直线方程式中即可求出直线解析式；
（2）根据题意知：点E的位置有三处．
（3）设点P运动t秒后PQ=2．由勾股定理可求出t的值，从而确定点P的坐标．
试题解析：（1）根据题意知：OB=8
∴A点坐标为（0，8）
设直线AB的解析式为y=kx+b
把A、B两点坐标代入得：
解得：
所以：直线AB的解析式为y=-x+8；
（2）（2）(8，8)、 (－8，8)、(8，－8)；
（3）(0，)、 (8－，2)．
考点：一次函数综合题
练习册系列答案
相关题目
中，一次函数
（a为常数）的图象与y轴相交于点A，与函数
的图象相交于点B
，
．
，
是任意两个不等实数，我们规定：满足不等式
≤
的实数
. 对于一个函数，如果它的自变量
满足：当m≤
上的“闭函数”.
是闭区间
上的“闭函数”吗？请判断并说明理由；
是闭区间
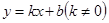是闭区间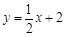
与坐标轴相交于A、B两点，与双曲线
交于点C．A、D两点关于y轴对称若四边形OBCD的面积为6，求k的值．
的图象在第四象限相交于点P，并且PA⊥x轴于点A，PB⊥y轴于点B，已知B（0，－6）且S△DBP＝27.
的图象与△ABP总有公共点，直接写出n的取值范围.
x＋6分别与x轴、y轴交于A、B两点；直线y＝
x与AB交于点C，与过点A且平行于y轴的直线交于点D．点E从点A出发，以每秒1个单位的速度沿
轴向左运动．过点E作x轴的垂线，分别交直线AB、OD于P、Q两点，以PQ为边向右作正方形PQMN，设正方形PQMN与△ACD重叠部分（阴影部分）的面积为S（平方单位），点E的运动时间为t（秒）．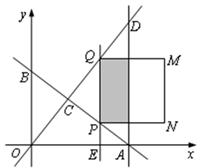
）在正方形PQMN内部时t的取值范围．
的图象与反比例函数
的图象交于A(1，4)、B(﹣2，m)两点， 
的解集．