题目内容
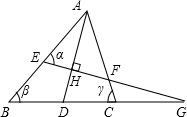 如图,AD平分∠BAC,EG⊥AD于H,则下列等式中成立的是
如图,AD平分∠BAC,EG⊥AD于H,则下列等式中成立的是
- A.∠α=
 (∠β+∠γ)
(∠β+∠γ) - B.∠α=
 (∠β-∠γ)
(∠β-∠γ) - C.∠G=
 (∠β+∠γ)
(∠β+∠γ) - D.∠G=
 ∠α
∠α
A
分析:由于∠α是△BEC的外角,可以得到∠α=∠β+∠G ①,而∠γ是△CFG的外角,可以得到∠γ=∠CFG+∠G ②,而∠AFE和∠CFG是对顶角,由∠AD平分∠BAC,EG⊥AD于H可以推出∠α=∠AFE,然后利用①②即可得到答案.
解答:∵∠α是△BEC的外角,
∴∠α=∠β+∠G ①,
∵∠γ是△CFG的外角,
∴∠γ=∠CFG+∠G ②
∵AD平分∠BAC,EG⊥AD于H,AH公共边,
∴△AEH≌△AFH,
∴AE=AF,
∴∠α=∠AFE,
而∠AFE=∠CFG,
∴∠AFE=∠CFG=∠α,
∴∠γ=∠α+∠G ③,
①-③得∠α-∠γ=∠β-∠α,
∴2∠α=∠β+∠γ,
即∠α= (∠β+∠γ).
(∠β+∠γ).
故选A.
点评:此题利用了全等三角形的判定与性质,三角形的内角和外角的关系等知识解题,综合性比较强.做题时,要结合已知条件与全等的判定方法对选项逐一验证.
分析:由于∠α是△BEC的外角,可以得到∠α=∠β+∠G ①,而∠γ是△CFG的外角,可以得到∠γ=∠CFG+∠G ②,而∠AFE和∠CFG是对顶角,由∠AD平分∠BAC,EG⊥AD于H可以推出∠α=∠AFE,然后利用①②即可得到答案.
解答:∵∠α是△BEC的外角,
∴∠α=∠β+∠G ①,
∵∠γ是△CFG的外角,
∴∠γ=∠CFG+∠G ②
∵AD平分∠BAC,EG⊥AD于H,AH公共边,
∴△AEH≌△AFH,
∴AE=AF,
∴∠α=∠AFE,
而∠AFE=∠CFG,
∴∠AFE=∠CFG=∠α,
∴∠γ=∠α+∠G ③,
①-③得∠α-∠γ=∠β-∠α,
∴2∠α=∠β+∠γ,
即∠α=
 (∠β+∠γ).
(∠β+∠γ).故选A.
点评:此题利用了全等三角形的判定与性质,三角形的内角和外角的关系等知识解题,综合性比较强.做题时,要结合已知条件与全等的判定方法对选项逐一验证.

练习册系列答案
相关题目
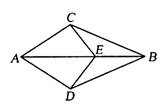
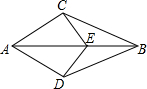 如图,AB平分∠CAD,E为AB上一点,若AC=AD,则下列结论错误的是( )
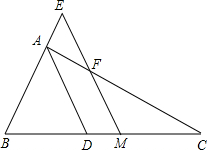
如图,AB平分∠CAD,E为AB上一点,若AC=AD,则下列结论错误的是( )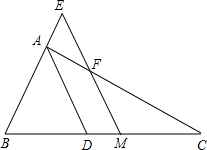 如图,AD为△ABC的角平分线,M为BC的中点,ME∥AD交BA的延长线于E,交AC于F.求证:BE=CF=
如图,AD为△ABC的角平分线,M为BC的中点,ME∥AD交BA的延长线于E,交AC于F.求证:BE=CF=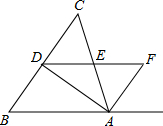 如图,AD是△ABC的角平分线,过点D作直线DF∥BA,交△ABC的外角平分线AF于点F,DF与AC交于点E.
如图,AD是△ABC的角平分线,过点D作直线DF∥BA,交△ABC的外角平分线AF于点F,DF与AC交于点E.