Question

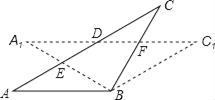
【题目】如图，△ABC中，∠A＝90°，D为AC上一点，E为BC上一点，点A和点E关于BD对称，点B和点C关于DE对称．求∠ABC和∠C的度数．

Answer 1

【答案】∠C＝30°,∠ABC＝60°．

【解析】

借助轴对称的性质，A点和E点关于BD对称，有∠ABD＝∠EBD，即∠ABC＝2∠ABD＝2∠EBD，B点、C点关于DE对称，可得∠DBE＝∠BCD，结合上式可得：∠ABC＝2∠BCD，且∠ABC＋∠BCD＝90°，进而求得∠ABC、∠C的值．

解：∵A点和E点关于BD对称，

∴∠ABD＝∠EBD，即∠ABC＝2∠ABD＝2∠EBD．

又B点、C点关于DE对称，

∴∠DBE＝∠C，∠ABC＝2∠C．

∵∠A＝90°，

∴∠ABC＋∠C＝2∠C＋∠C＝3∠C＝90°．

∴∠C＝30°

∴∠ABC＝2∠C＝60°．