题目内容
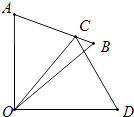
【题目】在Rt△OAB中，∠AOB=90°，已知AB= 
，AO：BO=1：3，将△OAB绕点O按顺时针方向旋转90°得到△ODC，如图1建立平面直角坐标系．
（1）求A，B，C三点坐标；
（2）若抛物线y=ax2+bx+c（a≠0）经过A，B，C三点（如图2），点P是抛物线的顶点，试判定△PCD的形状，并说明理由：
（3）在（2）的抛物线上，且在第一象限中，是否存在点Q，使S△QCD=S△OCD？若存在，请求点Q的横坐标；若不存在，请说明理由．
【答案】
（1）
解：在Rt△OAB中，AB= 
，AO：BO=1：3，
∴OA=1，OB=3，
∴A（﹣1，0），B（0，3），
∵△OCD是由△OAB绕点O按顺时针方向旋转90°所得，
∴OC=OB=3，
∴C（3，0），
综上可知A、B、C三点的坐标分别为（﹣1，0）、（0，3）、（3，0）；
（2）
解：∵抛物线经过A、C两点，
∴可设抛物线解析式为y=a（x+1）（x﹣3），
∵抛物线经过点B（0，3），
∴a（0+1）（0﹣3）=3，解得a=﹣1，
∴抛物线解析式为y=﹣（x+1）（x﹣3）=﹣（x﹣1）2+4，
∴P点坐标为（1，4），
∵OD=OA=1，
∴D（0，1），
∴PD= 
= ，CD= 
= ，PC= 
= 
=2 
，
∴PD2+CD2=PC2，且PD=CD，
∴△PCD是等腰直角三角形；
（3）
解：存在．
设直线CD解析式为y=kx+b，
∵直线经过点C（3，0），D（0，1），
∴ 
，解得 
，
∴直线CD解析式为y=﹣ 
x+1，
过点Q作QH∥y轴，交CD于点H，
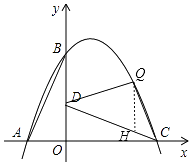
∵点Q是抛物线上第一象限内的点，
∴可设Q（m，﹣m2+2m+3）（m＞0），则点H为（m，﹣ m+1），
∴QM=﹣m2+2m+3﹣（﹣ m+1）=﹣m2+ 
m+2，
∴S△QCD= 
QMOC= （﹣m2+ m+2）×3=﹣ 
m2+ 
m+3，
∵S△QCD=S△OCD= ，
∴﹣ m2+ ，解得m= 
或m= 
（舍去），
∴存在满足条件的点Q，其横坐标为 ．
【解析】（1）在Rt△AOB中，根据条件可求得OA、OB的长，再由旋转的性质可求得OC的长，则可求得A、B、C的坐标；（2）由待定系数法可求得抛物线解析式，可求得P点坐标，结合D、C的坐标，可分别求得PD、PC、CD的长，则可判断出△PCD的形状；（3）可先求得直线CD解析式，过Q作QH∥y轴，交CD于点H，可设出Q点的坐标，从而可表示出QH，则可表示出△QCD的面积，由条件可得到方程，可求得Q点坐标．
【考点精析】通过灵活运用二次函数的图象和二次函数的性质，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小即可以解答此题．
