题目内容
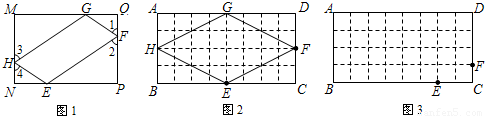
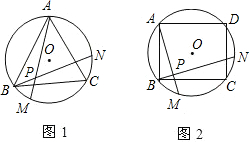
如图,图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动.(1)求图1中∠APN的度数是
(2)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
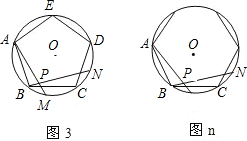
分析:根据对顶角相等和三角形内角和外角的关系解答即可.
解答:解:(1)图1:∵点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动,
∴∠BAM=∠CBN,
又∵∠APN=∠BPM,
∴∠APN=∠BPM=∠ABN+∠BAM=∠ABN+∠CBN=∠ABC=60°;
同理可得:在图2中,∠APN=90°;在图3中,∠APN=108°.
(2)由(1)可知,∠APN=所在多边形的内角度数,故在图n中,
.
∴∠BAM=∠CBN,
又∵∠APN=∠BPM,
∴∠APN=∠BPM=∠ABN+∠BAM=∠ABN+∠CBN=∠ABC=60°;
同理可得:在图2中,∠APN=90°;在图3中,∠APN=108°.
(2)由(1)可知,∠APN=所在多边形的内角度数,故在图n中,
| (n-2)180° |
| n |
点评:此题是一道规律探索题,体现了探索发现的一般规律:通过计算得出特殊多边形中的角∠APN的度数,然后得出n边形的∠APN的度数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目