题目内容
【题目】如图,在△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=55°,∠BDC=95°,求△BDE各内角的度数.
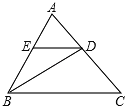
【答案】∠BDE=∠DBC=40°,∠BED=100°
【解析】
根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠ABD,再根据角平分线的定义可得∠DBC=∠ABD,然后根据两直线平行,内错角相等可得∠BDE=∠DBC,最后利用三角形的内角和定理列式计算求出∠BED.
∵∠A=55°,∠BDC=95°,
∴∠ABD=95°﹣55°=40°,
∵BD是∠ABC的角平分线,
∴∠DBC=∠ABD=40°,
∵DE∥BC,
∴∠BDE=∠DBC=40°,
在△BDE中,∠BED=180°﹣∠BDE﹣∠ABD=180°﹣40°﹣40°=100°.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目