题目内容
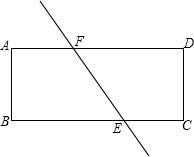
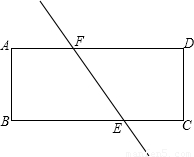
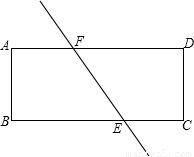
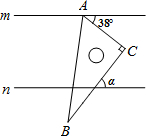如图，直线m∥n，直角三角板ABC的顶点A在直线m上，则∠α等于
- A.19°
- B.38°
- C.42°
- D.52°
D
分析：延长BC交直线m于D，根据三角形的外角性质求出∠ADC，根据平行线的性质得出∠ADC=∠α，代入即可求出答案．
解答：
延长BC交直线m于D，
∵∠ACB=90°，∠DAC=38°，
∴∠ADC=90°-38°=52°，
∵m∥n，
∴∠α=∠ADC=52°，
故选D．
点评：本题考查了平行线的性质和三角形的外角性质的应用，关键是正确作辅助线后求出∠ADC度数，注意：三角形的一个外角等于和它不相邻的两个内角之和，两直线平行，内错角相等．
分析：延长BC交直线m于D，根据三角形的外角性质求出∠ADC，根据平行线的性质得出∠ADC=∠α，代入即可求出答案．
解答：
延长BC交直线m于D，
∵∠ACB=90°，∠DAC=38°，
∴∠ADC=90°-38°=52°，
∵m∥n，
∴∠α=∠ADC=52°，
故选D．
点评：本题考查了平行线的性质和三角形的外角性质的应用，关键是正确作辅助线后求出∠ADC度数，注意：三角形的一个外角等于和它不相邻的两个内角之和，两直线平行，内错角相等．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
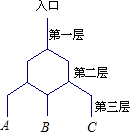如图所示是在竖直平面内的一个“通道游戏”．图中竖直线段和斜线段都表示通道，并且在交点处相遇，若竖直线段有一条的为第一层，有二条的为第二层，依此类推，现有一颗小弹子从第一层的通道里向下运动．并且小弹子落入每一条通道的可能性相同，则该小弹子从第三层通道的出口B脱出的概率为
