��Ŀ����
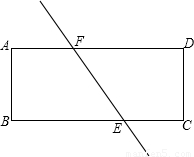
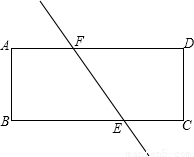
��ͼ��ֱ��EF������ֽƬABCD�ֳ������ȵ������֣�E��F�ֱ���BC���ڵ�E����AD���ڵ�F��E��F���붥���غϣ�����AB=a��AD=b��BE=x��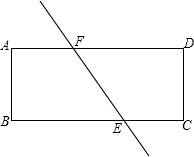
������֤��AF=EC��
�����ü�����ֽƬ��ֱ��EF�������ٽ�ֽƬABEF��AB�ԳƷ��ۣ�Ȼ��ƽ��ƴ��������ECDF���·���ʹһ�ױ��غϣ�ֱ�����ڱ�DC���ӳ����ϣ�ƴ�Ӻ��·������μ���EE��B��C��
��1�����ֱ��EE��ֱ�ԭ���εĶ���A�Ͷ���Dʱ������Ӧ��x��b��ֵ��
��2����ֱ��EE�侭��ԭ���ε�һ������������£�����BE�䣬ֱ��BE����EF�Ƿ�ƽ�У�������Ϊƽ�У������֤����������Ϊ��ƽ�У�����˵����a��b����ʲô��ϵʱ�����Ǵ�ֱ��
������������AB=a��AD=b��BE=x��S����ABEF=S����CDFE��������ε������ʽ��֤��AF=EC��
����1���������⣬����ͼ�Σ�������ε��������x��b��ֵ��
��2��ֱ��EE�侭��ԭ���εĶ���Dʱ����֤���ı���BE��EF��ƽ���ı��Σ���BE���EF����ֱ��EE�侭��ԭ���εĶ���Aʱ��BE����EF��ƽ�У�
����1���������⣬����ͼ�Σ�������ε��������x��b��ֵ��
��2��ֱ��EE�侭��ԭ���εĶ���Dʱ����֤���ı���BE��EF��ƽ���ı��Σ���BE���EF����ֱ��EE�侭��ԭ���εĶ���Aʱ��BE����EF��ƽ�У�
�������֤������AB=a��AD=b��BE=x��S����ABEF=S����CDFE��
��
a��x+AF��=
a��EC+b-AF����
��2AF=EC+��b-x����
�֡�EC=b-x��
��2AF=2EC��
��AF=EC��
���⣺��1����ֱ��EE�侭��ԭ���εĶ���Dʱ����ͼ��һ��
��EC��E��B�䣬
��
=
��
��EC=b-x��E��B��=EB=x��DB��=DC+CB��=2a��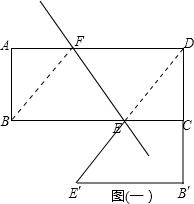
��
=
��
��x��b=
��
��ֱ��E��E����ԭ���εĶ���Aʱ����ͼ������
������AE��B��D��
��EC��E��B�䣬��C��DB����е㣬
��CE=
��AD+E��B�䣩��
��b-x=
��b+x����
��x��b=
��
��2����ͼ��һ������ֱ��EE�侭��ԭ���εĶ���Dʱ��BE���EF��
֤��������BF��
��FD��BE��FD=BE��
���ı���FBED��ƽ���ı��Σ�
��FB��DE��FB=DE��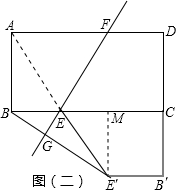
�֡�EC��E��B�䣬��C��DB����е㣬
��DE=EE�䣬
��FB��EE�䣬FB=EE�䣬
���ı���BE��EF��ƽ���ı��Σ�
��BE���EF��
��ͼ����������ֱ��EE�侭��ԭ���εĶ���Aʱ����ȻBE����EF��ƽ�У�
��ֱ��EF��BE�佻�ڵ�G������E����E��M��BC��M����E��M=a��
��x��b=
��
��EM=
BC=
b��
��BE����EF��ֱ�����С�GBE+��BEG=90�㣬
�֡ߡ�BEG=��FEC=��MEE�䣬��MEE��+��ME��E=90�㣬
���GBE=��ME��E��
��Rt��BME����tan��E��BM=tan��GBE=
=
��
��Rt��EME����tan��ME��E=
=
��
��
=
��
�֡�a��0��b��0��
=
��
�൱
=
ʱ��BE����EF��ֱ��
��
| 1 |
| 2 |
| 1 |
| 2 |
��2AF=EC+��b-x����
�֡�EC=b-x��
��2AF=2EC��
��AF=EC��
���⣺��1����ֱ��EE�侭��ԭ���εĶ���Dʱ����ͼ��һ��
��EC��E��B�䣬
��
| EC |
| E��B�� |
| DC |
| DB�� |
��EC=b-x��E��B��=EB=x��DB��=DC+CB��=2a��

��
| b-x |
| x |
| a |
| 2a |
��x��b=
| 2 |
| 3 |
��ֱ��E��E����ԭ���εĶ���Aʱ����ͼ������
������AE��B��D��
��EC��E��B�䣬��C��DB����е㣬
��CE=
| 1 |
| 2 |
��b-x=
| 1 |
| 2 |
��x��b=
| 1 |
| 3 |
��2����ͼ��һ������ֱ��EE�侭��ԭ���εĶ���Dʱ��BE���EF��
֤��������BF��
��FD��BE��FD=BE��
���ı���FBED��ƽ���ı��Σ�
��FB��DE��FB=DE��

�֡�EC��E��B�䣬��C��DB����е㣬
��DE=EE�䣬
��FB��EE�䣬FB=EE�䣬
���ı���BE��EF��ƽ���ı��Σ�
��BE���EF��
��ͼ����������ֱ��EE�侭��ԭ���εĶ���Aʱ����ȻBE����EF��ƽ�У�
��ֱ��EF��BE�佻�ڵ�G������E����E��M��BC��M����E��M=a��
��x��b=
| 1 |
| 3 |
��EM=
| 1 |
| 3 |
| 1 |
| 3 |
��BE����EF��ֱ�����С�GBE+��BEG=90�㣬
�֡ߡ�BEG=��FEC=��MEE�䣬��MEE��+��ME��E=90�㣬
���GBE=��ME��E��
��Rt��BME����tan��E��BM=tan��GBE=
| E��M |
| BM |
| a | ||
|
��Rt��EME����tan��ME��E=
| EM |
| E��M |
| ||
| a |
��
| a | ||
|
| ||
| a |
�֡�a��0��b��0��
| a |
| b |
| ||
| 3 |
�൱
| a |
| b |
| ||
| 3 |
�����������ǵ�����ƽ�Ƶ����ʡ����ε����ʺ�ƽ���ı��ε����ʽ�������ۺ��⣬���⸴�ӣ��Ѷȴ���ѧ���ۺ�������ѧ֪ʶ��������

��ϰ��ϵ�д�
�����Ŀ