题目内容
如图所示,已知直线y=-2x+12分别与y轴、x轴交于A、B两点,点M在y轴上,以点M为圆心的⊙M与直线AB相切于点D,连结MD.
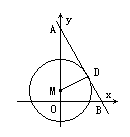
(1)求证:△ADM∽△AOB;
(2)如果⊙M的半径为2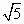 ,请求出点M的坐标,并求出以(-
,请求出点M的坐标,并求出以(-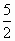 ,
,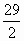 )为顶点,且过点M的抛物线的解析式;
)为顶点,且过点M的抛物线的解析式;
(3)在(2)的条件下,试问:在此抛物线上是否存在点P,使得以P、A、M三点为顶点的三角形与△AOB相似?如果存在,请求出所有符合条件的点P的坐标;如果不存在,请说明理由.
答案:
解析:
提示:
解析:
|
(1)易证 (2)y=-2x2-10x+2 (3)存在满足条件的点P.为P(-5,2)或P(-4,10). |
提示:
|
由两三角形相似,可求六种可能的点P,即P1(-20,12),P2(-5,12),P3(-20,2),P4(-5,2),P5(-4,10),P6(-4,4),其中只有P4(-5,2)和P5(-4,10)在抛物线上 |

练习册系列答案
相关题目
 三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由. 4、如图所示,已知直线a∥b,被直线L所截,如果∠1=69°36′,那么∠2=
4、如图所示,已知直线a∥b,被直线L所截,如果∠1=69°36′,那么∠2= 平移,设平移过程中△F′O′G′与四边形ODCE重叠部分面积为y,OO′的长为x(0≤x≤1),求y与x的函数关系式.
平移,设平移过程中△F′O′G′与四边形ODCE重叠部分面积为y,OO′的长为x(0≤x≤1),求y与x的函数关系式.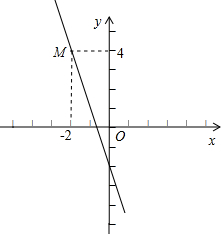 如图所示,已知直线y=kx-2经过M点,求此直线与x轴交点坐标和直线与两坐标轴围成三角形的面积.
如图所示,已知直线y=kx-2经过M点,求此直线与x轴交点坐标和直线与两坐标轴围成三角形的面积. 如图所示:已知直线y=
如图所示:已知直线y=