��Ŀ����
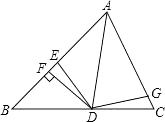
����Ŀ����ͼ������ABC�У���D��E�ֱ��ڱ�BC��AC�ϣ�����AD��DE������1=��B=��C��
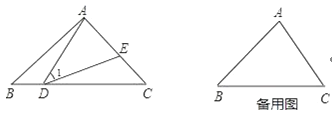
��1����������������д��������ȷ���ۣ���Ҫ��������������ĸ�����ߣ��ҽ��۹��������ӵ���ĸ�����߲��ܳ����ڽ����У�����֤����
�𣺽���һ�� ��
���۶��� ��
�������� ��
��2������B=45�㣬BC=2������D��BC���˶�ʱ����D����B��C�غϣ���
����CE�����ֵ��
������ADE�ǵ��������Σ����ʱBD�ij���
��ע�⣺�ڵڣ�2�����������У��������ã�1���еó��Ľ��ۣ������֤����
���𰸡���1��AB=AC����AED=��ADC����ADE�ס�ACD����2��
��������
�����������1������B=��C�����ݵ��������ε����ʿɵ�AB=AC������1=��C����AED=��EDC+��C�õ���AED=��ADC��������DAE=��CAD���������������ε��ж��ɵõ���ADE�ס�ACD��
��2��������B=��C����B=45��ɵ���ACBΪ����ֱ�������Σ���AC=![]() BC=
BC=![]() ��2=
��2=![]() ������1=��C����DAE=��CAD���������������ε��ж��ɵ���ADE�ס�ACD������AD��AC=AE��AD����AD2=AE
������1=��C����DAE=��CAD���������������ε��ж��ɵ���ADE�ס�ACD������AD��AC=AE��AD����AD2=AE ![]() AC��
AC��
AE=![]()
![]() AD2����AD��BC��AD������AD=
AD2����AD��BC��AD��С����AD=![]() BC=1����ʱAE��СΪ
BC=1����ʱAE��СΪ![]() ������CE=AC-AE�õ�CE�����ֵ��
������CE=AC-AE�õ�CE�����ֵ��
�����ۣ���AD=AEʱ������1=��AED=45�㣬�õ���DAE=90�㣬���D��B�غϣ�����������ȥ����EA=EDʱ����ͼ1������EAD=��1=45�㣬������ADƽ����BAC���õ�AD��ֱƽ��BC����BD=1��
��DA=DEʱ����ͼ2������ADE�ס�ACD������CADΪ���������Σ���DC=CA=![]() ��������BD=BC-DC=2-
��������BD=BC-DC=2-![]() ��
��
�����������1��AB=AC����AED=��ADC����ADE�ס�ACD��
��2���١ߡ�B=��C����B=45�㣬
���ACBΪ����ֱ�������Σ�
��AC=![]() BC=
BC=![]() ��2=
��2=![]() ��
��
�ߡ�1=��C����DAE=��CAD��
���ADE�ס�ACD��
��AD��AC=AE��AD����AD2=AE ![]() AC��
AC��
��AE=![]()
![]() AD2��
AD2��
��AD��Сʱ��AE��С����ʱAD��BC��AD=![]() BC=1��
BC=1��
��AE����СֵΪ![]() ��12=
��12=![]() ��
��
��CE�����ֵ=![]() -
-![]() =
=![]() ��
��
����AD=AEʱ��
���1=��AED=45�㣬
���DAE=90�㣬
����D��B�غϣ�����������ȥ��
��EA=EDʱ����ͼ1��
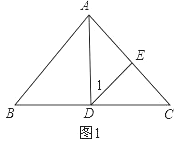
���EAD=��1=45�㣬
��ADƽ����BAC��
��AD��ֱƽ��BC��
��BD=1��
��DA=DEʱ����ͼ2��
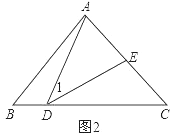
�ߡ�ADE�ס�ACD��
��DA��AC=DE��DC��
��DC=CA=![]() ��
��
��BD=BC-DC=2-![]() ��
��
����������������ADE�ǵ���������ʱ��BD�ij�Ϊ1��2-![]() ��
��