ЬтФПФкШн
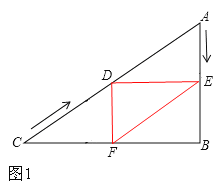
ЁОЬтФПЁПдкRtЁїABCжаЃЌЁЯB=90ЁуЃЌAC=60cmЃЌЁЯA=60ЁуЃЌЕуDДгЕуCГіЗЂбиCAЗНЯђвд4cm/УыЕФЫйЖШЯђЕуAдШЫйдЫЖЏЃЌЭЌЪБЕуEДгЕуAГіЗЂбиABЗНЯђвд2cm/УыЕФЫйЖШЯђЕуBдШЫйдЫЖЏЃЌЕБЦфжавЛИіЕуЕНДяжеЕуЪБЃЌСэвЛИіЕувВЫцжЎЭЃжЙдЫЖЏЃЎЩшЕуDЁЂEдЫЖЏЕФЪБМфЪЧtУыЃЈ0ЃМtЁм15ЃЉЃЎЙ§ЕуDзїDFЁЭBCгкЕуFЃЌСЌНгDEЃЌEFЃЎЃЈБИзЂЃКдкжБНЧШ§НЧаЮжа30ЖШНЧЫљЖдЕФБпЪЧаББпЕФвЛАыЃЉ
ЃЈ1ЃЉЧѓжЄЃКAE=DFЃЛ
ЃЈ2ЃЉЫФБпаЮAEFDФмЙЛГЩЮЊСтаЮТ№ЃПШчЙћФмЃЌЧѓГіЯргІЕФtжЕЃЌШчЙћВЛФмЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБtЮЊКЮжЕЪБЃЌЁїDEFЮЊжБНЧШ§НЧаЮЃПЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЁЂжЄУїЙ§ГЬМћНтЮіЃЛЃЈ2ЃЉЁЂt=10ЃЛЃЈ3ЃЉЁЂt=![]() Лђ12ЃЌРэгЩМћНтЮі
Лђ12ЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉЁЂИљОнRtЁїABCЕФаджЪЕУГіAB=30cmЃЌИљОнCD=4tЃЌAE=2tвдМАRtЁїCDFЕФаджЪЕУГіД№АИЃЛЃЈ2ЃЉЁЂИљОнDFЁЮABЃЌDF=AEЃЌЕУГіЫФБпаЮAEFDЪЧЦНааЫФБпаЮЃЌИљОнСтаЮЕФаджЪЕУГіtЕФжЕЃЛЃЈ3ЃЉЁЂБОЬташвЊЗжСНжжЧщПіЗжБ№НјааМЦЫу.ЕБЁЯEDF=90ЁуЪБЃЌAD=2AEЃЌДгЖјЧѓГіtЕФжЕЃЛЕБЁЯDEF=90ЁуЪБЃЌAE=2ADЃЌДгЖјЧѓГіtЕФжЕ.
ЪдЬтНтЮіЃКЃЈ1ЃЉЁЂЁпдкRtЁїABCжаЃЌЁЯC=90ЁуЉЁЯA=30ЁуЃЌ ЁрAB=![]() AC=
AC=![]() ЁС60=30cm
ЁС60=30cm
ЁпCD=4tЃЌAE=2tЃЌ гжЁпдкRtЁїCDFжаЃЌЁЯC=30ЁуЃЌЁрDF=![]() CD=2t ЁрDF=AE
CD=2t ЁрDF=AE
ЃЈ2ЃЉЁЂФмЁЃ
ЁпDFЁЮABЃЌDF=AEЃЌЁрЫФБпаЮAEFDЪЧЦНааЫФБпаЮ
ЕБAD=AEЪБЃЌЫФБпаЮAEFDЪЧСтаЮЃЌМД60Љ4t=2tЃЌНтЕУЃКt=10
ЁрЕБt=10ЪБЃЌAEFDЪЧСтаЮ
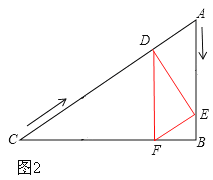
ЃЈ3ЃЉЁЂШєЁїDEFЮЊжБНЧШ§НЧаЮЃЌгаСНжжЧщПіЃК
ЂйШчЭМ1ЃЌЁЯEDF=90ЁуЃЌDEЁЮBCЃЌ
дђAD=2AEЃЌМД60Љ4t=2ЁС2tЃЌНтЕУЃКt=![]() ЁЃ
ЁЃ
ЂкШчЭМ2ЃЌЁЯDEF=90ЁуЃЌDEЁЭACЃЌ
дђAE=2ADЃЌМД2t=2ЃЈ60-4tЃЉЃЌНтЕУЃКt=12ЁЃ
злЩЯЫљЪіЃЌЕБt=![]() Лђ12ЪБЃЌЁїDEFЮЊжБНЧШ§НЧаЮ
Лђ12ЪБЃЌЁїDEFЮЊжБНЧШ§НЧаЮ

 УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ