题目内容
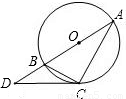
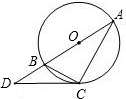 已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.
已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.(1)求证:CD为⊙O的切线;
(2)过点C作CE⊥AB于E,若CE=2,cosD=
| 4 | 5 |
分析:(1)要证DC是⊙O的切线,只要连接OC,再证OC⊥CD即可.
(2)根据三角函数知识即可求出⊙O的半径.
(2)根据三角函数知识即可求出⊙O的半径.
解答: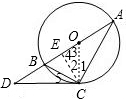 证明:(1)连接CO,(1分)
证明:(1)连接CO,(1分)
∵AB是⊙O直径,
∴∠1+∠OCB=90°.
∵AO=CO,
∴∠1=∠A.
∵∠5=∠A,
∴∠5+∠OCB=90°.
即∠OCD=90°,
∴OC⊥CD.
又∵OC是⊙O半径,
∴CD为⊙O的切线.(3分)
(2)∵OC⊥CD于C,
∴∠3+∠D=90°.
∵CE⊥AB于E,
∴∠3+∠2=90°.
∴∠2=∠D.
∴cos∠2=cosD.(4分)
在△OCD中,∠OCD=90°,
∴cos∠2=
.
∵cosD=
,CE=2,
∴
=
.
∴CO=
.
∴⊙O的半径为
.(5分)
 证明:(1)连接CO,(1分)
证明:(1)连接CO,(1分)∵AB是⊙O直径,
∴∠1+∠OCB=90°.
∵AO=CO,
∴∠1=∠A.
∵∠5=∠A,
∴∠5+∠OCB=90°.
即∠OCD=90°,
∴OC⊥CD.
又∵OC是⊙O半径,
∴CD为⊙O的切线.(3分)
(2)∵OC⊥CD于C,
∴∠3+∠D=90°.
∵CE⊥AB于E,
∴∠3+∠2=90°.
∴∠2=∠D.
∴cos∠2=cosD.(4分)
在△OCD中,∠OCD=90°,
∴cos∠2=
| CE |
| CO |
∵cosD=
| 4 |
| 5 |
∴
| 2 |
| CO |
| 4 |
| 5 |
∴CO=
| 5 |
| 2 |
∴⊙O的半径为
| 5 |
| 2 |
点评:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.同时考查了三角函数的知识.

练习册系列答案
相关题目
 (2012•黔南州)已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.
(2012•黔南州)已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.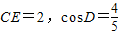 ,求⊙O的半径.
,求⊙O的半径.
 ,求⊙O的半径.
,求⊙O的半径.