题目内容
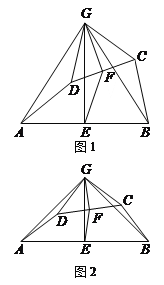
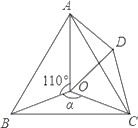
【题目】如图,在△ABC中,AB=AC=4,∠BAC=90°,点D在边AB上,BE∥CD,AE⊥CD,垂足为F,且EF=2,点G在线段CF上,若∠GAF=45°,则△ACG的面积为_____.

【答案】![]() ﹣1
﹣1
【解析】
首先证明△CAF≌△ABE,推出AE=CF,设AF=x,则CF=AE=x+2,在Rt△ACF中,根据AC2=AF2+CF2,可得42=x2+(x+2)2,求出x即可解决问题;
∴∠AFD=∠AEB=∠AFC=90,
∴∠CAF+∠EAB=90,∠EAB+∠ABE=90,
∴∠CAF=∠ABE,
∵AC=AB,
∴△CAF≌△ABE,
∴AE=CF,设AF=x,则CF=AE=x+2,
在Rt△ACF中,∵AC2=AF2+CF2,
∴42=x2+(x+2)2,
∴x=1+![]() 或1
或1![]() (舍弃)
(舍弃)
∵∠GAF=45,∠AFG=90
∴AF=FG=![]() 1,CG=CFFG=1+
1,CG=CFFG=1+![]() (
(![]() 1)=2,
1)=2,
∴S△AGC=![]() CGAF=
CGAF=![]() 1,
1,
故答案为:![]() ﹣1
﹣1

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目