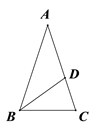题目内容
【题目】如图,在△ABC中, AB的垂直平分线EF交BC于点E,交AB于点F, D为线段CE的中点, BE=AC.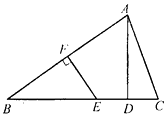
(1)求证: ![]()
(2)若 ![]() ,求∠B的度数.
,求∠B的度数.
【答案】
(1)解:连接AE,
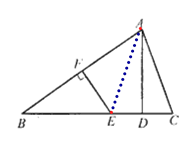
∵EF垂直平分AB,
∴AE=BE ,
∵BE=AC,
∴AE=AC,
∵D是EC的中点,
∴AD⊥BC.
(2)解:设∠B=x°,
∵AE=BE,
∴∠BAD=∠B=x,
∴∠AEC=2x,
∵AE=AC,
∴∠C=∠AEC=2x,
在三角形ABC中,3x+75°=180°.
x=35. ∴∠B=35°.
【解析】(1)根据垂直平分线的性质,线段垂直平分线上的点与线段的两个端点的距离相等;得到AE=AC,由D是EC的中点,根据等腰三角形的三线合一,得到AD⊥BC;(2)根据三角形内角和定理直接求出∠B的度数.

练习册系列答案
相关题目