题目内容
如图（9）在∠AOB内有一点P，点M、N分别是点P关于OA、OB的对称点，MN分别交OA、OB于C、D点，若△PCD周长为30cm，则线段MN长为 。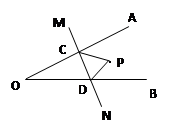
MN=30cm
利用对称性得到CM=PC，DN=PD，把求MN的长转化成△PCD的周长，问题得解．
解：∵点P关于OA、OB的对称点分别为C、D，
∴MC=PC，ND=PD，
∴MN=CM+CD+ND=PC+CD+PD=30cm．
本题考查轴对称的性质，对称轴上的任何一点到两个对应点之间的距离相等．
解：∵点P关于OA、OB的对称点分别为C、D，
∴MC=PC，ND=PD，
∴MN=CM+CD+ND=PC+CD+PD=30cm．
本题考查轴对称的性质，对称轴上的任何一点到两个对应点之间的距离相等．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
） 
