题目内容
【题目】定义:点M,N把线段AB分割成AM、MN,NB,若以AM、MN、NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.
(1)如图①,已知M、N是线段AB的勾股分割点,AM=6,MN=8,求NB的长;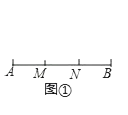
(2)如图②,在△ABC中,点D、E在边线段BC上,且BD=3,DE=5,EC=4,直线l∥BC,分别交AB、AD、AE、AC于点F、M、N、G.求证:点M,N是线段FG的勾股分割点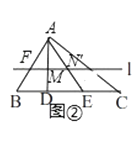
(3)在菱形ABCD中,∠ABC=β(β<90°),点E、F分别在BC、CD上,AE、AF分别交BD于点M、N.
①如图③,若BE= ![]() BC,DF=
BC,DF= ![]() CD,求证:M、N是线段BD的勾股分割点.
CD,求证:M、N是线段BD的勾股分割点.
②如图④,若∠EAF= ![]() ∠BAD,sinβ=
∠BAD,sinβ= ![]() ,当点M、N是线段AB的勾股分割点时,求BM:MN:ND的值.
,当点M、N是线段AB的勾股分割点时,求BM:MN:ND的值.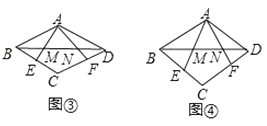
【答案】
(1)
解:当NB为最长线段时,
∵M、N是线段AB的勾股分割点,AM=6,MN=8,
∴NB= ![]() =10;
=10;
当MN为最长线段时,
NB= ![]() =2
=2 ![]() ,
,
综上所述,NB的值为10或2 ![]() ;
;
(2)
证明:如图2,∵BD=3,DE=5,EC=4,
∴DE2=BD2+EC2,
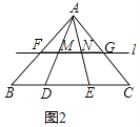
∵直线l∥BC,
∴![]() ,
,
∴可设![]() ,
,
∴FM=kBD,MN=kDE,NG=kEC,
∵DE2=BD2+EC2,
∴MN2=FM2+NG2,
∴点M,N是线段FG的勾股分割点;
(3)
解:①证明:如图3,∵四边形ABCD是菱形,
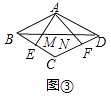
∴AD//BE,AB=BC=CD=DA,
∴△BEM∽△DAM,
∴![]() ,
,
∵BE=![]() BC,
BC,
∴BM=![]() DM,BM=
DM,BM=![]() BD,
BD,
同理可得,DN=![]() BD,
BD,
∴MN=BD﹣BM﹣DN=![]() BD,
BD,
∵MN2=![]() BD2,BM2+ND2=
BD2,BM2+ND2=![]() BD2+
BD2+![]() BD2=
BD2=![]() BD2,
BD2,
∴MN2=BM2+ND2,
∴M、N是线段BD的勾股分割点.
②如图4,将△AND绕点A顺时针旋转,旋转角等于∠BAD,则AD旋转后与AB重合,点N旋转至点K的位置,DN=BK,∠ADN=∠ABK,连接KM,
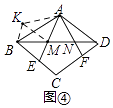
∴∠KBM=∠KBA+∠ABM=∠ABC,
∵sinβ=![]() ,
,
∴sin∠KBM=![]() ,
,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠KAM=∠NAM,
∵AN=AK,AM=AM,
∴△KAM≌△NAM,
∴KM=NM,
∵点M、N是线段BD的勾股分割点,
∴△KBM是直角三角形,
∵sin∠KBM=![]() ,
,
∴BM:MN:ND=13:12:5或BM:MN:ND=5:12:13.
【解析】(1)分两种情况进行讨论:NB为最长线段;MN为最长线段,分别根据勾股定理进行计算即可;(2)根据BD=3,DE=5,EC=4,可得DE2=BD2+EC2 , 再根据直线l∥BC,可得 ![]() =
= ![]() ,故可设
,故可设 ![]() =
= ![]() =
= ![]() =k,进而得到FM=kBD,MN=kDE,NG=kEC,再根据DE2=BD2+EC2 , 可得MN2=FM2+NG2 , 即点M,N是线段FG的勾股分割点;(3)①先判定△BEM∽△DAM,得出
=k,进而得到FM=kBD,MN=kDE,NG=kEC,再根据DE2=BD2+EC2 , 可得MN2=FM2+NG2 , 即点M,N是线段FG的勾股分割点;(3)①先判定△BEM∽△DAM,得出 ![]() =
= ![]() ,再根据BE=
,再根据BE= ![]() BC,可得出BM=
BC,可得出BM= ![]() DM,BM=
DM,BM= ![]() BD,同理可得,DN=
BD,同理可得,DN= ![]() BD,进而得到MN=BD﹣BM﹣DN=
BD,进而得到MN=BD﹣BM﹣DN= ![]() BD,再根据MN2=BM2+ND2 , 可得M、N是线段BD的勾股分割点.②将△AND绕点A顺时针旋转,旋转角等于∠BAD,则AD旋转后与AB重合,点N旋转至点K的位置,DN=BK,∠ADN=∠ABK,连接KM,先判定△KAM≌△NAM,即可得出KM=NM,再根据点M、N是线段BD的勾股分割点,可得△KBM是直角三角形,再根据sin∠KBM=
BD,再根据MN2=BM2+ND2 , 可得M、N是线段BD的勾股分割点.②将△AND绕点A顺时针旋转,旋转角等于∠BAD,则AD旋转后与AB重合,点N旋转至点K的位置,DN=BK,∠ADN=∠ABK,连接KM,先判定△KAM≌△NAM,即可得出KM=NM,再根据点M、N是线段BD的勾股分割点,可得△KBM是直角三角形,再根据sin∠KBM= ![]() ,可得BM:MN:ND=13:12:5或BM:MN:ND=5:12:13.
,可得BM:MN:ND=13:12:5或BM:MN:ND=5:12:13.
【考点精析】通过灵活运用勾股定理的概念和图形的旋转,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素即可以解答此题.

【题目】网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:
关注情况 | 频数 | 频率 |
A.高度关注 | 50 | b |
B.一般关注 | 120 | 0.6 |
C.不关注 | a | 0.1 |
D.不知道 | 10 | 0.05 |
(1)根据上述统计图可得此次采访的人数为人,a= , b=;
(2)根据以上信息补全条形统计图; 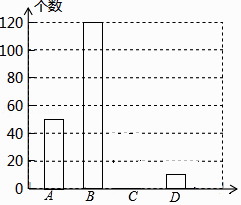
(3)根据上述采访结果,请估计在6400名市民中,高度关注售后评价的市民约有多少人?


