题目内容
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交与点
轴交与点![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 坐标为
坐标为![]() ,抛物线的对称轴方程为
,抛物线的对称轴方程为![]() .
.
(![]() )求抛物线的解析式.
)求抛物线的解析式.
(![]() )点
)点![]() 从
从![]() 点出发,在线段
点出发,在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向
个单位长度的速度向![]() 点运动,同时点
点运动,同时点![]() 从
从![]() 点出发,在线段
点出发,在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向
个单位长度的速度向![]() 点运动,其中一个点到达终点时,另一个点也停止运动,在点
点运动,其中一个点到达终点时,另一个点也停止运动,在点![]() 运动过程中,是否存在某一时刻
运动过程中,是否存在某一时刻![]() ,使
,使![]() 为直角三角形?若存在,求出
为直角三角形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(![]() )若点
)若点![]() 为抛物线对称轴上一点,当
为抛物线对称轴上一点,当![]() 是直角三角形时,求点
是直角三角形时,求点![]() 的坐标.
的坐标.

【答案】(![]() )抛物线的解析式为
)抛物线的解析式为![]() ;
;
(![]() )
)![]() 或
或![]() 时,
时, ![]() 为直角三角形;
为直角三角形;
(![]() )
)![]() 点坐标为
点坐标为![]() ,
, ![]() ,
,  ,
, 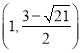 .
.
【解析】试题分析: ![]() 把点
把点![]() 的坐标分别代入抛物线解析式,列出关于系数
的坐标分别代入抛物线解析式,列出关于系数![]() 的解析式,通过解方程组求得它们的值;
的解析式,通过解方程组求得它们的值;
![]() 分
分![]() 和
和![]() 两种情况进行讨论.
两种情况进行讨论.
![]() 分三种情况进行讨论.
分三种情况进行讨论.
试题解析:(![]() )∵点
)∵点![]() 坐标为
坐标为![]() 抛物线对称轴方程为
抛物线对称轴方程为![]() ,
,
∴![]() ,
,
把![]() ,
, ![]() ,
, ![]() 代入
代入![]() 中,
中,
解得 ,
,
∴抛物线的解析式为![]() .
.
(![]() )
)
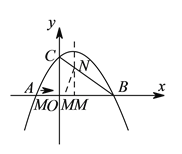
①当![]() 时,
时,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 秒之后,
秒之后, ![]() ,
,
∴![]() ,
,
∵![]() 是直角三角形,
是直角三角形,
![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
②当![]() 时,
时,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]()
![]() ,
,
∴![]() 或
或![]() 时,
时, ![]() 为直角三角形.
为直角三角形.
(![]() )设
)设![]() 点坐标为
点坐标为![]() ,
,
①若![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() 点坐标为
点坐标为![]() .
.
②若![]() ,
,
∴![]() ,
,
即![]()
![]() ,
,
∴![]() 点坐标为
点坐标为![]() .
.
③若![]() ,
,
即![]() ,
,
![]() .
.
![]() ,
,
∴![]() 点坐标为
点坐标为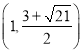 或
或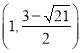 .
.
综上所述, ![]() 点坐标为
点坐标为![]() ,
, ![]() ,
, 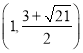 ,
, 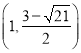 .
.

练习册系列答案
相关题目