题目内容
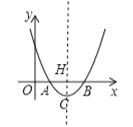
【题目】如图，已知抛物线y=x2﹣4x+3与x轴交于A，B两点，其顶点为C．
（1）对于任意实数m，点M（m，﹣2）是否在该抛物线上？请说明理由；
（2）求证：△ABC是等腰直角三角形；
（3）若点D在x轴上，则在抛物线上是否存在点P，使得PD∥BC，且PD=BC？若存在，求点P的坐标；若不存在，请说明理由．
【答案】（1）不在；（2）答案见解析；（3）（
，1）或（
，1）．
【解析】试题分析：（1）假如点M（m，﹣2）在该抛物线上，则﹣2=m2﹣4m+3，通过变形为：m2﹣4m+5=0，由根的判别式就可以得出结论；
（2）如图，根据抛物线的解析式求出点C的坐标，再利用勾股定理求出AB、AC和BC的值，由勾股定理的逆定理就可以得出结论．
（3）假设存在点P，根据对角线互相平分的四边形是平行四边形，因此连接点P与点C的线段应被x轴平分，就可以求得P点的纵坐标为1，代入抛物线的解析式就可以求出P点的横坐标．
试题解析：解：（1）假如点M（m，﹣2）在该抛物线上，∴﹣2=m2﹣4m+3，∴m2﹣4m+5=0，∴△=（﹣4）2﹣4×1×5=﹣4＜0，∴此方程无实数解，∴点M（m，﹣2）不会在该抛物线上；
（2）过点C作CH⊥x轴，交x轴与点H，连接CA、CB．如图，当y=0时，x2﹣4x+3=0，x1=1，x2=3．∵点A在点B左侧，∴A（1，0），B（3，0），∴OA=1，OB=3，∴AB=2．
∵y=x2﹣4x+3，∴y=（x﹣2）2﹣1，∴C（2，﹣1），∴AH=BH=CH=1．
在Rt△AHC和Rt△BHC中，由勾股定理得，AC=
，BC=
，∴AC2+BC2=AB2，∴△ABC是等腰直角三角形；
（3）存在这样的点P．
∵PD∥BC，PD=BC，∴四边形PBCD是平行四边形，∴根据对角线互相平分的四边形是平行四边形，因此连接点P与点C的线段应被x轴平分，∴点P的纵坐标是1．∵点P在抛物线y=x2﹣4x+3上，∴x2﹣4x+3=1，解得x1=2﹣
，x2=2+
，∴点P的坐标是（2﹣
，1）或（2+
，1）．
