题目内容
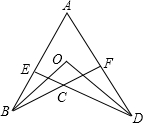 如图,已知∠A+∠BCD=140°,BO平分∠ABC,DO平分∠ADC,则∠BOD=( )
如图,已知∠A+∠BCD=140°,BO平分∠ABC,DO平分∠ADC,则∠BOD=( )| A、40° | B、60° | C、70° | D、80° |
分析:根据三角形的一个外角等于和它不相邻的两个内角的和∠BFD=∠A+∠ABC,所以∠BCD=∠A+∠ABC+∠ADC,再根据角平分线的定义和三角形外角性质∠BOD=∠A+
∠ABC+
∠ADC,代入数据即可求解.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:在△ABF中,∠BFD=∠A+∠ABC,
解:在△ABF中,∠BFD=∠A+∠ABC,
在△CFD中,∠BCD=∠BFD+∠ADC=∠A+∠ABC+∠ADC,
∴∠A+∠BCD=∠A+∠A+∠ABC+∠ADC=140°,
连接AO并延长,
根据三角形的外角性质,
∵BO平分∠ABC,DO平分∠ADC,
∠BOD=∠ABO+∠ADO+∠A=
(∠ABC+∠ADC)+∠A=140°÷2=70°.
故选C.
 解:在△ABF中,∠BFD=∠A+∠ABC,
解:在△ABF中,∠BFD=∠A+∠ABC,在△CFD中,∠BCD=∠BFD+∠ADC=∠A+∠ABC+∠ADC,
∴∠A+∠BCD=∠A+∠A+∠ABC+∠ADC=140°,
连接AO并延长,
根据三角形的外角性质,
∵BO平分∠ABC,DO平分∠ADC,
∠BOD=∠ABO+∠ADO+∠A=
| 1 |
| 2 |
故选C.
点评:本题主要考查三角形的一个外角等于和它不相邻的两个内角的和的性质,熟练掌握性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 =2,∠ADC=30°
=2,∠ADC=30° 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=