题目内容
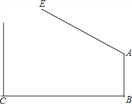
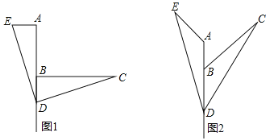
【题目】如图1,已知∠ABC=![]() ,D是直线AB上的一点,AD=BC,连结DC.以DC为边,在∠CDB的同侧作∠CDE,使得∠CDE=∠ABC,并截取DE=CD,连结AE.
,D是直线AB上的一点,AD=BC,连结DC.以DC为边,在∠CDB的同侧作∠CDE,使得∠CDE=∠ABC,并截取DE=CD,连结AE.
(1)求证:![]() ;并判断AE和BC的位置关系,说明理由;
;并判断AE和BC的位置关系,说明理由;
(2)若将题目中的条件“∠ABC=900”改成“∠ABC=x0(0<x<180)”,
①结论“![]() ”还成立吗?请说明理由;②试探索:当
”还成立吗?请说明理由;②试探索:当![]() 的值为多少时,直线AE⊥BC.
的值为多少时,直线AE⊥BC.
【答案】(1)见解析,AE∥BC,见解析;(2)①成立,见解析;②x=45°或135°时,AE⊥BC.
【解析】
(1)根据已知条件得到∠CBD=90°,根据全等三角形的判定定理得到Rt△BDC≌Rt△ADE,由全等三角形的性质得到∠A=∠CBD=90°,即可得到结论;
(2)①根据三角形外角的性质得∠C=∠ADE,根据全等三角形的判定定理即可得到△BDC≌△AED;
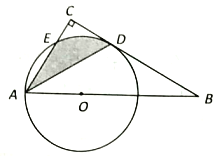
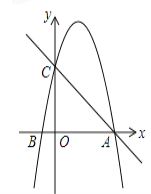
②如图2,延长EA交BC于F,根据全等三角形的性质得到∠DBC=∠EAD然后根据等腰直角三角形的性质即可得到结论;如图3时,同理得到∠ABC=135°,由此即可得答案.
(1)AE∥BC,
理由:∵∠CDE=∠ABC=90°,
∴∠CBD=90°,
在Rt△BDC与Rt△AED中,
![]() ,
,
∴Rt△BDC≌Rt△AED,
∴∠A=∠CBD=90°,
∴∠A=∠ABC=90°,
∴AE∥BC;
(2)①成立,∵∠CDE=∠ABC=x°,
∴∠C+∠CDB=∠ADE+∠CDB=x°,
∴∠C=∠ADE,
在△BDC与△AED中,
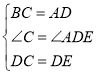 ,
,
∴△BDC≌△AED;
②如图2,延长EA交BC于F,
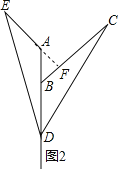
∵△BDC≌△AED,
∴∠DBC=∠EAD,
∴∠FAB=∠ABF,
∴当AE⊥BC时,
即∠AFB=90°,
∴∠FAB+∠ABF=90°,
∴∠ABC=45°,
如图3,同理得到∠ABC=135°,

∴当x=45或135°时,AE⊥BC.

 应用题作业本系列答案
应用题作业本系列答案