Question

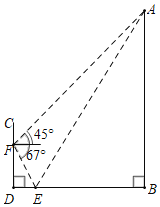
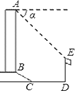
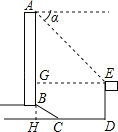
【题目】如图，某办公大楼正前方有一根高度是15米的旗杆ED，从办公大楼顶端A测得旗杆顶端E的俯角α是45°，旗杆底端D到大楼前梯坎底边的距离DC是20米，梯坎坡长BC是12米，梯坎坡度i＝1：，则大楼AB的高度为________米．（精确到0.1米，参考数据：，，）

Answer 1

【答案】6+29

【解析】

延长AB交DC于H，作EG⊥AB于G，则GH＝DE＝15米，EG＝DH，设BH＝x米，则CH＝x米，在Rt△BCH中，BC＝12米，由勾股定理得出方程，解方程求出BH＝6米，CH＝6米，得出BG、EG的长度，证明△AEG是等腰直角三角形，得出AG＝EG＝6+20（米），即可得出大楼AB的高度．

延长AB交DC于H，作EG⊥AB于G，如图所示：

则GH＝DE＝15米，EG＝DH，

∵梯坎坡度i＝1：，

∴BH：CH＝1：，

设BH＝x米，则CH＝x米，

在Rt△BCH中，BC＝12米，

由勾股定理得：x2+（x）2＝122，

解得：x＝6，

∴BH＝6米，CH＝6米，

∴BG＝GH﹣BH＝15﹣6＝9（米），EG＝DH＝CH+CD＝6+20（米），

∵∠α＝45°，

∴∠EAG＝90°﹣45°＝45°，

∴△AEG是等腰直角三角形，

∴AG＝EG＝6+20（米），

∴AB＝AG+BG＝6+20+9＝（6+29）m．

故答案为：6+29．