题目内容
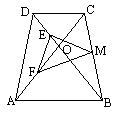
如图,等腰梯形ABCD中,AB∥CD,AB>CD,AD=BC,对角线AC、BD交于O,∠AOB=![]() ,且E、F分别是OD、OA的中点,M是BC的中点,求证:△EFM是等边三角形.
,且E、F分别是OD、OA的中点,M是BC的中点,求证:△EFM是等边三角形.
答案:
解析:
解析:
|
证明:∵AD=BC,∠DAB=∠CBA,AB=AB, ∴△DAB≌CBA. ∴∠DBA=∠CAB. 即△OAB为等腰三角形.
∵∠AOB= ∴△AOB是等边三角形. 连结BF,因F是OA的中点,所以BF⊥AO,即△BFC为直角三角形. 又∵M是BC的中点, ∴FM= 在△AOD中,E、F分别是OD、OA的中点. ∴EF= ∴EF=EM=FM. ∴△EFM是等边三角形. |

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目

 14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( )
14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( ) 24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC.
24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC. (2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=
(2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD= 如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm. 如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.