题目内容
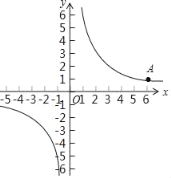
【题目】在平面直角坐标系xOy中,反比例函数y=![]() 的图象过点A(6,1).
的图象过点A(6,1).
(1)求反比例函数的表达式;
(2)过点A的直线与反比例函数y=![]() 图象的另一个交点为B,与y轴交于点P,若AP=3PB,求点B的坐标.
图象的另一个交点为B,与y轴交于点P,若AP=3PB,求点B的坐标.
【答案】(1)![]() ;(2)B点坐标为(2,3)或(﹣2,﹣3)
;(2)B点坐标为(2,3)或(﹣2,﹣3)
【解析】
(1)由点A的坐标利用反比例函数图象上点的坐标特征即可求出m值,从而得出反比例函数表达式;
(2)过A点作AM⊥y轴于点M,AM=6,作BN⊥y轴于点N,则AM∥BN,由平行线的性质结合AP=3PB即可求出BN的长度,从而得出点B的横坐标,再利用反比例函数图象上点的坐标特征即可求出点B的坐标.
(1)反比例函数y=![]() 的图象过点A(6,1),
的图象过点A(6,1),
∴m=6×1=6,
∴反比例函数的表达式为y=![]() ;
;
(2)过A点作AM⊥y轴于点M,AM=6,作BN⊥y轴于点N,则AM∥BN,如图所示,

∵AM∥BN,AP=3PB,
∴![]() ,
,
∵AM=6,
∴BN=2,
∴B点横坐标为2或﹣2,
∴B点坐标为(2,3)或(﹣2,﹣3).

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目