题目内容
已知：如图，在等边△ABC中取点P，使得PA，PB，PC的长分别为3，4，5，将线段AP以点A为旋转中心顺时针旋转60°到线段AD，连接BD，下列结论：①△ABD可以由△APC绕点A顺时针旋转60°得到；②点P与点D的距离为3；③∠APB=150°；④S△APC+S△APB=6+
| 9 |
| 4 |
| 3 |
其中正确的结论有（ ）
分析：①由旋转的性质、等边三角形的性质以及全等三角形的判定定理SAS证得△ADP≌△APC，即△ABD可以由△APC绕点A顺时针旋转60°得到；
②连接PD．根据①中的旋转的性质知△APD是等边三角形；
③利用勾股定理的逆定理可得△PBD为直角三角形，且∠BPD=90°，则∠APB=∠APD+∠BPD=60°+90°=150°；
④由△ADB≌△APC得S△ADB=S△APC，则有S△APC+S△APB=S△ADB+S△APB=S△ADP+S△BPD，根据等边三角形的面积为边长平方的
倍和直角三角形的面积公式即可得到S△ADP+S△BPD=
×32+
×3×4=6+
②连接PD．根据①中的旋转的性质知△APD是等边三角形；
③利用勾股定理的逆定理可得△PBD为直角三角形，且∠BPD=90°，则∠APB=∠APD+∠BPD=60°+90°=150°；
④由△ADB≌△APC得S△ADB=S△APC，则有S△APC+S△APB=S△ADB+S△APB=S△ADP+S△BPD，根据等边三角形的面积为边长平方的
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| 3 |
解答：解：连PD，如图，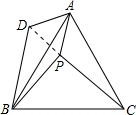
∵线段AP以点A为旋转中心顺时针旋转60°得到线段AD，
∴AD=AP，∠DAP=60°，
又∵△ABC为等边三角形，
∴∠BAC=60°，AB=AC，
∴∠DAB+∠BAP=∠PAC+∠BAP，
∴∠DAP=∠PAC，
∴△ABD可以由△APC绕点A顺时针旋转60°得到，所以①正确；
∵DA=PA，∠DAP=60°，
∴△ADP为等边三角形，
∴PD=PA=3，所以②正确；
在△PBD中，PB=4，PD=3，由①得到BD=PC=5，
∵32+42=52，即PD2+PB2=BD2，
∴△PBD为直角三角形，且∠BPD=90°，
由②得∠APD=60°，
∴∠APB=∠APD+∠BPD=60°+90°=150°，所以③正确；
∵△ADB≌△APC，
∴S△ADB=S△APC，
∴S△APC+S△APB=S△ADB+S△APB=S△ADP+S△BPD=
×32+
×3×4=6+
，所以④正确．
故选D．
∵线段AP以点A为旋转中心顺时针旋转60°得到线段AD，
∴AD=AP，∠DAP=60°，
又∵△ABC为等边三角形，
∴∠BAC=60°，AB=AC，
∴∠DAB+∠BAP=∠PAC+∠BAP，
∴∠DAP=∠PAC，
∴△ABD可以由△APC绕点A顺时针旋转60°得到，所以①正确；
∵DA=PA，∠DAP=60°，
∴△ADP为等边三角形，
∴PD=PA=3，所以②正确；
在△PBD中，PB=4，PD=3，由①得到BD=PC=5，
∵32+42=52，即PD2+PB2=BD2，
∴△PBD为直角三角形，且∠BPD=90°，
由②得∠APD=60°，
∴∠APB=∠APD+∠BPD=60°+90°=150°，所以③正确；
∵△ADB≌△APC，
∴S△ADB=S△APC，
∴S△APC+S△APB=S△ADB+S△APB=S△ADP+S△BPD=
| ||
| 4 |
| 1 |
| 2 |
9
| ||
| 4 |
故选D．
点评：本题考查了旋转的性质：旋转前后两图形全等，即对应角线段，对应线段线段；对应点的连线段所夹的角等于旋转角；对应点到旋转中心的距离相等．也考查了等边三角形的判定与性质、勾股定理的逆定理．
练习册系列答案
阅读快车系列答案
相关题目
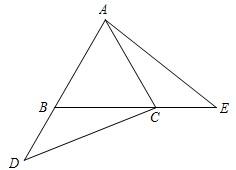23、已知：如图，在等边三角形ABC中，点D、E分别在边AB、BC的延长线上，且AD=BE，连接AE、CD．
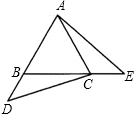已知：如图，在等边三角形ABC中，点D、E分别是AB、BC延长线上的点，且BD=CE．
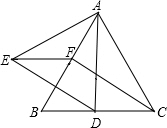已知：如图，在等边△ABC中，D、F分别为CB、BA上的点，且CD=BF，以AD为边作等边三角形ADE．求证：
已知：如图，在等边三角形ABC的三边上，分别取点D，E，F使AD=BE=CF．