Question

【题目】在平行四边形ABCD中，E，F分别为边AB，CD的中点，连接DE，BF，BD．

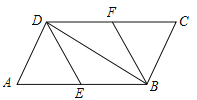
（1）求证：△ADE≌△CBF．

（2）若AD⊥BD，则四边形BFDE是什么特殊四边形？请证明你的结论．

Answer 1

【答案】(1)、证明过程见解析；(2)、菱形；证明过程见解析.

【解析】

试题分析：(1)、根据平行四边形的性质得到AD=BC，AB=CD，∠A=∠C，根据中点得到AE=CF，从而说明三角形全等；(2)、首先判断BFDE为平行四边形，根据直角三角形斜边上的中线的性质得到DE=BE，从而说明四边形BFDE为菱形.

试题解析：(1)、∵四边形ABCD为平行四边形 ∴AD=BC AB=CD ∠A=∠C

∵E，F分别为AB，CD的中点 ∴AE=CF ∴△ADE≌△CBF

、∵ABCD为平行四边形，E，F分别为AB，CD的中点 ∴DF=BE DF∥BE

∴四边形BFDE为平行四边形 ∵AD⊥BD ∴△ABD为直角三角形 DE为三角形斜边上的中线

∴DE=BE ∴四边形BFDE为菱形.