题目内容
【题目】阅读理解填空,并在括号内填注理由.如图,已知AB//CD,M,N分别交AB,CD于点E,F,![]() ,求证:EP//FQ.
,求证:EP//FQ.
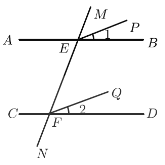
证明:![]() AB//CD(_________),
AB//CD(_________),
![]() (__________).
(__________).
又![]() (_____________)
(_____________)
∴![]() (___________)
(___________)
即:![]() ( )
( )
∴EP//______.(________).
【答案】见解析.
【解析】
根据两直线平行,同位角相等可得∠MEB=∠MFD,由两角的差根据等式的性质可得 ∠MEP=∠MFQ,再根据同位角相等,两直线平行即可证得结论.
∵AB//CD(已知),
∴∠MEB=∠MFD(两直线平行,同位角相等),
又∵∠1=∠2(已知),
∠MEB-∠1=∠MFD-∠2(等式性质),
即:∠MEP=∠MFQ,
∴EP//FQ(同位角相等,两直线平行),
故答案为:已知;两直线平行,同位角相等;已知;等式性质;MFQ;FQ;同位角相等,两直线平行.

练习册系列答案
相关题目
【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为![]() ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
|
| 0.32 |
|
|
|
| 10 | 0.1 |
合计 | 100 | 1 |
书法作品比赛成绩频数直方图

根据上述信息,解答下列问题:
(1)请你把表中空白处的数据填写完整.
(2)请补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级的幅数.