��Ŀ����
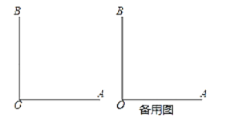
����Ŀ����ͼ��P���߶�AB��һ�㣬AB��12cm��C��D����ֱ��P��B������1cm/s��2cm/s���ٶ�ͬʱ��ֱ��AB�����˶���C���߶�AP�ϣ�D���߶�BP�ϣ����˶�ʱ��Ϊts
��I����C��D�˶�1sʱ����PD��2AC����AP�ij���
��II����C��D�˶�����һʱ��ʱ������PD��2AC��AP�ij����Ƿ�仯�������䣬�����AP�ij������仯����˵�����ɣ�
��III���ڣ�II���������£�Q��ֱ��AB��һ�㣬��AQ��BQ��PQ����PQ�ij���
![]()
���𰸡�����PA��4cm�������Ȳ������仯��AP��4cm������PQ��4cm��12cm��
��������
������AC+CP+PD+BD��AB���г����̿���AC�ij���������⣻
�������߶εĺͲ��ϵ����⣻
���������軭��ͼʾ������AQ��BQ��PQ���AQ��PQ+BQ��Ȼ�����AP��BQ���Ӷ����PQ��AB�Ĺ�ϵ��
�⣺������C��D���˶��ٶȿ�֪��BD��2cm��PC��1cm��
��AC+CP+PD+BD��AB����PD��2AC��
��AC+1+2AC+2��12��
��AC��3cm��
��PA��4ccm��
�����Ȳ������仯��
�������£�
����C��D���˶��ٶȿ�֪��BD��2PC��
��AC+CP+PD+BD��AB����PD��2AC��
��3AC+3PC��12��
��AP��4cm��
������ͼ��
![]()
��AQ��BQ��PQ��
��AQ��PQ+BQ��
�֡�AQ��AP+PQ��
��AP��BQ��
��PQ��![]() AB��4cm��
AB��4cm��
����Q'��AB���ӳ�����ʱ��
AQ�䩁AP��PQ�䣬
����AQ�䩁BQ�䣽PQ��AB��12cm��
����������PQ��4cm��12cm��

����Ŀ��ɽ�����г�Խ��Խ�ܵ���ѧ����ϲ��������Ʒ�����Ͷ���г���ij���о�Ӫ��A�ͳ�ȥ�������ܶ�Ϊ5��Ԫ������ÿ�����ۼ۱�ȥ�꽵��400Ԫ����������������ͬ�������ܶ��ȥ�����20%��
��1������A�ͳ�ÿ���ۼ۶���Ԫ�������з��̵ķ������
��2���ó��мƻ��½�һ��A�ͳ����¿�B�ͳ���60������B�ͳ��Ľ�������������A�ͳ�������������Ӧ��ν�������ʹ������������ࣿ
A��B�����ͺų��Ľ��������ۼ۸����±���
A�ͳ� | B�ͳ� | |
�����۸�Ԫ�� | 1100 | 1400 |
���ۼ۸�Ԫ�� | ��������ۼ۸� | 2000 |