题目内容
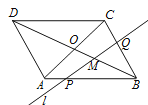
【题目】如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),
且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.
(1)求证:OM=ON;
(2)若正方形ABCD的边长为6,OE=EM,求MN的长.

【答案】(1)见解析;(2)MN![]() .
.
【解析】
(1)证△OAM≌△OBN即可得;
(2)作OH⊥AD,由正方形的边长为6且E为OM的中点知OH=HA=3、HM=6,再根据勾股定理得OM=![]() ,由勾股定理即可求出MN的长.
,由勾股定理即可求出MN的长.
(1)∵四边形ABCD是正方形,
∴OA=OB,∠DAO=45°,∠OBA=45°,
∴∠OAM=∠OBN=135°,
∵∠EOF=90°,∠AOB=90°,
∴∠AOM=∠BON,
∴△OAM≌△OBN(ASA),
∴OM=ON;
(2)如图,过点O作OH⊥AD于点H,

∵正方形的边长为6,
∴OH=HA=3,
∵E为OM的中点,
∴HM=6,
则OM=![]() ,
,
∴MN=![]()
![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
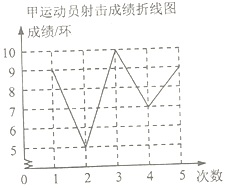
【题目】第16届省运会在我市隆重举行,推动了我市各校体育活动如火如荼的开展,在某校射箭队的一次训练中,甲,乙两名运动员前5箭的平均成绩相同,教练将两人的成绩绘制成如下尚不完整的统计图表.
乙运动员成绩统计表(单位:环)
第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
8 | 10 | 8 | 6 |
|
(1)甲运动员前5箭射击成绩的众数是 环,中位数是 环;
(2)求乙运动员第5次的成绩;
(3)如果从中选择一个成绩稳定的运动员参加全市中学生比赛,你认为应选谁去?请说明理由.