题目内容
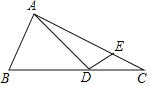
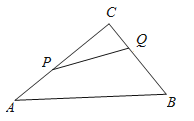
【题目】如图，△ABC中，∠C=90°，BC=6cm，AC=8cm，点P从点A开始沿AC向点C以2厘米/秒的速度运动；与此同时，点Q从点C开始沿CB边向点B以1厘米/秒的速度运动；如果P、Q分别从A、C同时出发，当其中一点到达终点时，另一点也随之停止运动．
（1）经过几秒，△CPQ的面积等于3cm2？
（2）在整个运动过程中，是否存在某一时刻t，使PQ恰好平分△ABC的面积？若存在，求出运动时间t；若不存在，请说明理由．
（3）是否存在某一时刻，PQ长为
，如果存在，求出运动时间t。
【答案】（1）1或3秒；（2）不存在满足条件的t；（3）
【解析】
（1）设出运动所求的时间，可将BP和BQ的长表示出来，代入三角形面积公式，列出等式，可将时间求出；
（2）将△PBQ的面积表示出来，根据△=b2-4ac来判断；
（3）设经过y秒后存在，则PC＝8－2y,CQ=y,根据勾股定理可得PC2+CQ2=(
)2,求方程即可.
（1）解：设经过x秒，△CPQ的面积等于3cm2．则
x（8﹣2x）=3，
化简得x2﹣4x+3=0，
解得x1=1，x2=3；
（2）设存在某一时刻t，使PQ恰好平分△ABC的面积．则
t（8﹣2t）=××6×8，
化简得t2﹣4t+12=0，
b2﹣4ac=16﹣48=﹣32＜0，
故方程无实数根，即不存在满足条件的t．
（3）设经过y秒后存在PQ长为，则PC＝8－2y,CQ=y,
∵∠C=90°，
∴PC2+CQ2=()2,
解得：y1=,y2=5(不符合题意，舍去),
所以经过秒后，PQ的长为.
【题目】吴京同学根据学习函数的经验，对一个新函数y＝
的图象和性质进行了如下探究，请帮他把探究过程补充完整
（1）该函数的自变量x的取值范围是 ．
（2）列表：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … |
| m | ﹣1 |
| ﹣5 | n | ﹣1 |
|
| … |
表中m＝ ，n＝ ．
（3）描点、连线
在下面的格点图中，建立适当的平面直角坐标系xOy中，描出上表中各对对值为坐标的点（其中x为横坐标，y为纵坐标），并根据描出的点画出该函数的图象：
（4）观察所画出的函数图象，写出该函数的两条性质：
① ；
② ．
