题目内容
在锐角△ABC中,∠A,∠B,∠C的对边分别是a,b,c.如图所示,过C作CD⊥AB于D,则cosA=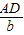 ,
,即AD=bcosA.
∴BD=c-AD=c-bcosA
在Rt△ADC和Rt△BDC中有CD2=AC2-AD2=BC2-BD2
∴b2-b2cos2A=a2-(c-bcosA)2
整理得:a2=b2+c2-2bccosA
同理可得:b2=a2+c2-2accosB
c2=a2+b2-2abcosC
这个结论就是著名的余弦定理,在以上三个等式中有六个元素a,b,c,∠A,∠B,∠C,若已知其中的任意三个元素,可求出其余的另外三个元素.
如:在锐角△ABC中,已知∠A=60°,b=3,c=6,
则由(1)式可得:a2=32+62-2×3×6cos60°=27
∴a=3
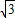 ,∠B,∠C则可由式子(2)、(3)分别求出,在此略.
,∠B,∠C则可由式子(2)、(3)分别求出,在此略.根据以上阅读理解,请你试着解决如下问题:
已知锐角△ABC的三边a,b,c分别是7,8,9,求∠A,∠B,∠C的度数.(保留整数)

【答案】分析:此题只要把三边代入余弦定理即可求出三角的余弦值,从而求出三角.
解答:解:由(1)得:72=82+92-2×8×9cosA
则cosA=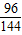 ,∠A≈48°
,∠A≈48°
由(2)得:82=92+72-2×9×7cosB
则cosB=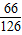 ,∠B≈58°
,∠B≈58°
∴∠C=180°-∠A-∠B=74°.
点评:代入法是数学中常用的一种方法,学生一定要牢固掌握.
解答:解:由(1)得:72=82+92-2×8×9cosA
则cosA=
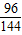 ,∠A≈48°
,∠A≈48°由(2)得:82=92+72-2×9×7cosB
则cosB=
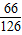 ,∠B≈58°
,∠B≈58°∴∠C=180°-∠A-∠B=74°.
点评:代入法是数学中常用的一种方法,学生一定要牢固掌握.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
在锐角△ABC中,a、b、c分别表示为∠A、∠B、∠C的对边,O为其外心,则O点到三边的距离之比为( )
| A、a:b:c | ||||||
B、
| ||||||
| C、cosA:cosB:cosC | ||||||
| D、sinA:sinB:sinC |
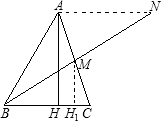 在锐角△ABC中,最大的高线AH等于中线BM,求证:∠B<60°(如图).
在锐角△ABC中,最大的高线AH等于中线BM,求证:∠B<60°(如图). 如图,在锐角△ABC中,∠BAC=60°,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①B、E、D、C四点共圆;②AD•AC=AE•AB;③△DEF是等边三角形;④当∠ABC=45°时,BE=
如图,在锐角△ABC中,∠BAC=60°,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①B、E、D、C四点共圆;②AD•AC=AE•AB;③△DEF是等边三角形;④当∠ABC=45°时,BE=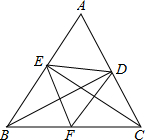 (2013•南开区一模)在锐角△ABC中,∠BAC=60°,BD、CE为高,F是BC的中点,连接DE、EF、FD,则以下结论中一定正确的个数有( )
(2013•南开区一模)在锐角△ABC中,∠BAC=60°,BD、CE为高,F是BC的中点,连接DE、EF、FD,则以下结论中一定正确的个数有( )