题目内容
如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
(1)
(2)﹣1<x<0或x>1。
(3)首先求出OA的长度,结合题意CB∥OA且CB= ,判断出四边形OABC是平行四边形,再证明OA=OC。
,判断出四边形OABC是平行四边形,再证明OA=OC。
解析分析:(1)设反比例函数的解析式为 (k>0),然后根据条件求出A点坐标,再求出k的值,进而求出反比例函数的解析式。
(k>0),然后根据条件求出A点坐标,再求出k的值,进而求出反比例函数的解析式。
(2)直接由图象得出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)首先求出OA的长度,结合题意CB∥OA且CB= ,判断出四边形OABC是平行四边形,再证明OA=OC
,判断出四边形OABC是平行四边形,再证明OA=OC
解:(1)设反比例函数的解析式为 (k>0)
(k>0)
∵A(m,﹣2)在y=2x上,∴﹣2=2m,∴解得m=﹣1。∴A(﹣1,﹣2)。
又∵点A在 上,∴
上,∴ ,解得k=2。,
,解得k=2。,
∴反比例函数的解析式为 。
。
(2)观察图象可知正比例函数值大于反比例函数值时自变量x的取值范围为﹣1<x<0或x>1。
(3)四边形OABC是菱形。证明如下:
∵A(﹣1,﹣2),∴ 。
。
由题意知:CB∥OA且CB= ,∴CB=OA。
,∴CB=OA。
∴四边形OABC是平行四边形。
∵C(2,n)在 上,∴
上,∴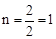 。∴C(2,1)。
。∴C(2,1)。
∴ 。∴OC=OA。
。∴OC=OA。
∴平行四边形OABC是菱形。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
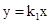 的图象于反比例函数
的图象于反比例函数 的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式。
的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式。
 与双曲线
与双曲线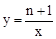 交于C、D两点,与x轴交于点A.
交于C、D两点,与x轴交于点A.
 ,求点C和点D的坐标并根据图象直接写出反比例函数的值小于一次函数的值时,自变量x的取值范围.
,求点C和点D的坐标并根据图象直接写出反比例函数的值小于一次函数的值时,自变量x的取值范围.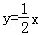 的图象与反比例函数
的图象与反比例函数 (k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.
(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.
 的图象是由反比例函数
的图象是由反比例函数 的图象向左平移2个单位长度得到.灵活运用这一知识解决问题.
的图象向左平移2个单位长度得到.灵活运用这一知识解决问题. 的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B.
的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B. 的解集.
的解集.