题目内容
【题目】如图,∠A=90°,∠AOB=30°,AB=2,△A′OB′可以看作是由△AOB绕点O逆时针旋转60°得到的,求点A′与点B的距离
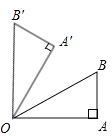
【答案】2.
【解析】试题分析:根据图形旋转的性质可得出OA=OA′,∠A′OA=60°,又知∠AOB=30°,可得∠A′OB=30°,再根据全等三角形的判定定理可得出△AOB≌△A′OB,由全等三角形的性质即可得出结论.
试题解析:
解:连接A′B,

∵△A′OB′可以看作是由△AOB绕点O逆时针旋转60°得到的,
∴△AOB≌△A′OB′,
∴OA=OA′,
∴∠A′OA=60°,
∵∠AOB=30°,AB=2,
∴∠A′OB=30°,
在△AOB与△A′OB中,
OA=OA′,∠A′OB=∠AOB,OB=OB,
∴△AOB≌△A′OB,
∴A′B=AB=2.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目