题目内容
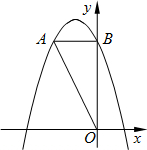
如图,抛物线y=-x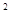 +4x+5交x轴于A、B(以A左B右)两点,交y轴于点C.
+4x+5交x轴于A、B(以A左B右)两点,交y轴于点C.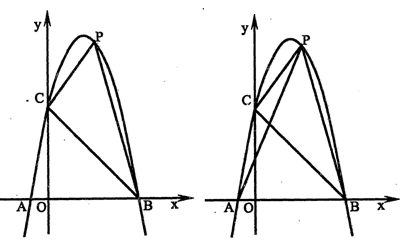
(1)求直线BC的解析式;
(2)点P为抛物线第一象限函数图象上一点,设P点的横坐标为m,△PBC的面积为S,求S与m的函数关系式;
(3)在(2)的条件下,连接AP,抛物线上是否存在这样的点P,使得线段PA被BC平分,如果不存在,请说明理由;如果存在,求点P的坐标.
(1) y=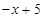 (2) S=
(2) S=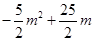 (3)存在,P(2,9)或P(3,8)
(3)存在,P(2,9)或P(3,8)
解析试题分析:(1)令y=0,解关于x的一元二次方程即可得到点A、B的坐标,再令x=0求出点C的坐标,设直线BC解析式为y=kx+b(k≠0),利用待定系数法求一次函数解析式解答;
(2)过点P作PH⊥x轴于H,交BC于F,根据抛物线和直线BC的解析式表示出PF,再根据S△PBC=S△PCF+S△PBF整理即可得解;
(3)设AP、BC的交点为E,过点E作EG⊥x轴于G,根据垂直于同一直线的两直线平行可得EG∥PH,然后判断出△AGE和△AHP相似,根据相似三角形对应边成比例可表示出EG、HG,然后表示出BG,根据OB=OC可得∠OCB=∠OBC=45°,再根据等角对等边可得EG=BG,然后列出方程求出m的值,再根据抛物线解析式求出点P的纵坐标,即可得解.
试题解析:(1)当y=0时,x1=5,x2=-1,
∵A左B右,
∴A(-1,0),B(5,O)
当x=0时,y=5,
∴C(0,5),
设直线BC解析式为y=kx+b,
∴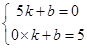
∴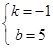
∴直线BC解析式为:y=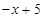 ;
;
(2)作PH⊥x轴于H,交BC于点F,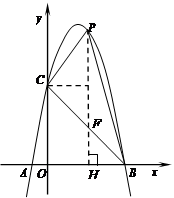
P(m,-m2+4m+5),F(m,-m+5)
PF=-m2+5m ,
S△PBC=S△PCF+S△PBF
S=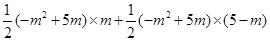
∴S=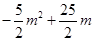 ;
;
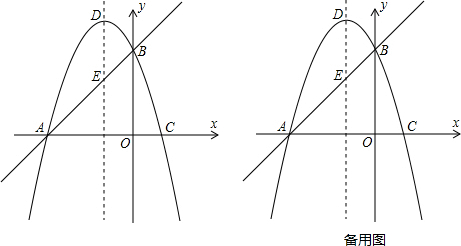
(3)存在点P,
作EG⊥AB于G,PH⊥AB于H,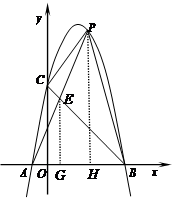
∴EG∥PH,
∴△AGE∽△AHP,
∴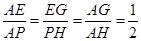 ,
,
∵P(m,-m2+4m+5),
EG=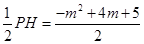 ,
,
AH=m-(-1)=m+1, GH=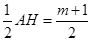 ,
,
HB="5-m" ,GB=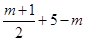 ,
,
∵OC=OB=5,
∴∠OCB=∠OBC=45°,
∴EG=BG,
∴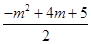 =
=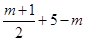 ,
,
∴m1=2 m2=3,
当m=2时,P(2,9),
当m=3时,P(3,8),
∴存在这样的点P, 使得线段PA被BC平分,P(2,9)或P(3,8).
考点:二次函数综合题.



 ),那么:
),那么: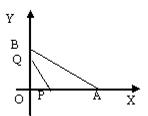
 ,求
,求 的函数解析式。
的函数解析式。