题目内容
 已知:如图,Rt△ABC中,∠ACB=90°,点O在AC上,以O为圆心、OC为半径的圆与AB相切于点D,交AC于点E.
已知:如图,Rt△ABC中,∠ACB=90°,点O在AC上,以O为圆心、OC为半径的圆与AB相切于点D,交AC于点E.
(1)求证:DE∥OB;
(2)若⊙O的半径为2,BC=4,求AD的长.
 (1)证明:∵∠ACB=90°,CO是⊙O的半径,
(1)证明:∵∠ACB=90°,CO是⊙O的半径,∴BC是⊙O的切线,
又∵AB与⊙O相切,
∴OC=OD,且BO为∠CBA的角平分线,
∴BO⊥CD,
又∵CE是⊙O的直径,且C是⊙O上一点,
∴DE⊥CD,
∴DE∥OB;
(2)解:∵DE∥OB,
∴
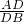 =
= ,
,又BD=BC=4,OE=2,
∴
 =
= ,即AD=2AE,
,即AD=2AE,又AD、AC分别是⊙O的切线和割线,
∴AD2=AE•AC,即AD2=AE•(AE+4),
∴AD2=
 •(
•( +4),可得AD=
+4),可得AD= .
.分析:(1)根据AB与⊙O相切,BC是⊙O的切线,结合等腰三角形的性质判断出BO⊥CD,根据直径所对的圆周角是90°,判断出ED⊥CD,得出DE∥OB;
(2)因为DE∥OB,根据平行线分线段成比例定理,确定AD和AE的关系,再根据切割线定理,可求出AD的长.
点评:此题是一道基础性题目,考查了和圆相关的等腰三角形的性质、切线长定理以及平行线分线段成比例定理,仔细分析,建立起它们之间的关系即可解答.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 22、已知:如图,Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,试以图中标有字母的点为端点,连接两条线段,如果你所连接的两条线段满足相等,垂直或平行关系中的一种,那么请你把它写出来并证明.
22、已知:如图,Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,试以图中标有字母的点为端点,连接两条线段,如果你所连接的两条线段满足相等,垂直或平行关系中的一种,那么请你把它写出来并证明. 20、已知:如图,Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD,连接DE、DC.
20、已知:如图,Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD,连接DE、DC.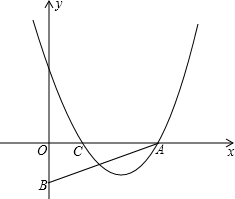 C=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常数且m+2≥2p>0)经过A、C两点.
C=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常数且m+2≥2p>0)经过A、C两点.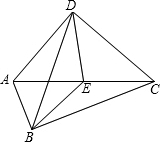 已知:如图,Rt△ABC和Rt△ADC,∠ABC=∠ADC=90°,点E是AC的中点.
已知:如图,Rt△ABC和Rt△ADC,∠ABC=∠ADC=90°,点E是AC的中点.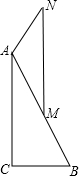 已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AM=AN,MN∥AC.
已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AM=AN,MN∥AC.