题目内容
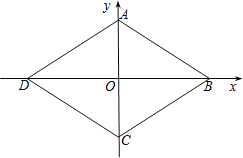
【题目】如图,在平面直角坐标系中,菱形ABCD的四个顶点均在坐标轴上,A(0,2),∠ABC=60°.把一条长为2013个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A﹣…的规律紧绕在菱形ABCD的边上,则细线另一端所在位置的点的坐标是( )
A.(![]()
![]() ,
,![]() ) B.(
) B.(![]()
![]() ,﹣
,﹣![]() ) C.(﹣
) C.(﹣![]()
![]() ,
,![]() ) D.(﹣
) D.(﹣![]() ,
,![]()
![]() )
)
【答案】C
【解析】
试题分析:根据A的坐标和∠ABC=60°,求出菱形的边长和周长,然后求出另一端是绕第几圈后的第几个单位长度,从而确定答案.
解:∵A(0,2),
∴AC=4,
∵∠ABC=60°,
∴AB=BC=CD=DA=4,菱形的周长为16,
即绕菱形ABCD一周的细线长度为16,
2013÷16=125…13,
则细线另一端在绕四边形第125圈的第13个单位长度的位置,
即此时细线另一端在AD边上,且距离D点为1个单位长度,距离A点3个单位长度,
设AD所在的直线为y=kx+b,
∵∠ABC=60°,A(0,2),
∴D(﹣2![]() ,0),
,0),
把点的坐标代入求解析式得:y=﹣![]() x+2,
x+2,
即CD所在直线为y=﹣![]() x+2,
x+2,
把选项中各点代入,满足题意的为(﹣![]()
![]() ,
,![]() ).
).
故选C.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目