题目内容
 如图,已知线段AB与线段CD关于某一点成中心对称,请在图中画出此对称中心,并判断线段AB与CD是否平行?并用所学过的知识说明理由.
如图,已知线段AB与线段CD关于某一点成中心对称,请在图中画出此对称中心,并判断线段AB与CD是否平行?并用所学过的知识说明理由.
解:如图所示,点O即为对称中心.
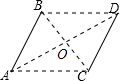
∵线段AB与线段CD成中心对称,
∴BC过对称中心,AD过对称中心,
∴AD、BC的交点即为对称中心;
∵线段AB与线段CD关于点O成中心对称,
∴OA=OD,OB=OC,
∴四边形ABDC是平行四边形,
∴线段AB与CD平行.
分析:先根据中心对称的性质,连接任意两对对应点,交点即为对称中心,可知连接AD与BC的交点O即为对称中心,再根据中心对称的性质得出四边形ABDC的对角线互相平分,则四边形ABDC是平行四边形,从而判断出线段AB与CD平行.
点评:本题考查了利用旋转变换作图,中心对称图形的性质,是基础题,比较简单,熟记性质是解题的关键.

∵线段AB与线段CD成中心对称,
∴BC过对称中心,AD过对称中心,
∴AD、BC的交点即为对称中心;
∵线段AB与线段CD关于点O成中心对称,
∴OA=OD,OB=OC,
∴四边形ABDC是平行四边形,
∴线段AB与CD平行.
分析:先根据中心对称的性质,连接任意两对对应点,交点即为对称中心,可知连接AD与BC的交点O即为对称中心,再根据中心对称的性质得出四边形ABDC的对角线互相平分,则四边形ABDC是平行四边形,从而判断出线段AB与CD平行.
点评:本题考查了利用旋转变换作图,中心对称图形的性质,是基础题,比较简单,熟记性质是解题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目

 20、如图,已知线段AB与P、Q两点,
20、如图,已知线段AB与P、Q两点,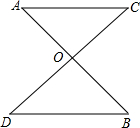 如图,已知线段AB与CD相交于点O,且点O是线段AB的中点,要使△AOC≌△BOD,还需补充一个条件是
如图,已知线段AB与CD相交于点O,且点O是线段AB的中点,要使△AOC≌△BOD,还需补充一个条件是 如图,已知线段AB与线段CD关于某一点成中心对称,请在图中画出此对称中心,并判断线段AB与CD是否平行?并用所学过的知识说明理由.
如图,已知线段AB与线段CD关于某一点成中心对称,请在图中画出此对称中心,并判断线段AB与CD是否平行?并用所学过的知识说明理由.